Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai mặt phẳng (A’B’CD) và (ABC’D’) bằng
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai mặt phẳng (A’B’CD) và (ABC’D’) bằng
Những câu hỏi liên quan
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai mặt phẳng ( A’B’CD) và (ABC’D’) bằng A.
30
0
B.
60
0
C.
45
0
D.
90
0
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai mặt phẳng ( A’B’CD) và (ABC’D’) bằng
A. 30 0
B. 60 0
C. 45 0
D. 90 0
Cho hình lập phương ABCD.A’B’C’D’. Gọi α là góc giữa đường thẳng A’C và mặt phẳng (ABC’D’). Khi đó: A.
tanα
3
B.
tanα
1
C.
tanα
1
3
D.
tanα
2
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’. Gọi α là góc giữa đường thẳng A’C và mặt phẳng (ABC’D’). Khi đó:
A. tanα = 3
B. tanα = 1
C. tanα = 1 3
D. tanα = 2
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có BC=a, B B ' = a 3 . Góc giữa hai mặt phẳng (A’B’C) và (ABC’D’) bằng
A. 60°.
B. 30°.
C. 45°.
D. 90°.
Cho hình hộp ABCD.A’B’C’D’. Gọi O, O’ lần lượt là tâm của hai mặt ADD’A’ và BCC’B’. Tìm giao tuyến của hai mặt (ABC’D’) và (A’B’CD)?
A. BD’
B. A’C
C. OO’
D. AC.
Đáp án C
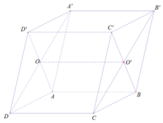
Ta có: C’B ∩ CB’ = O '
⇒ O’ là điểm chung của (A’B’CD) và (ABC’D’)
A’D ∩ AD’ = O
⇒ O là điểm chung của (A’B’CD) và (ABC’D’)
⇒ OO’ là giao tuyến cần tìm
Đúng 0
Bình luận (0)
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai mặt phẳng (ABCD) và (A’B’C’D’) bằng A.
45
°
.
B.
60
°
.
C.
0
°
.
D.
90
°
.
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai mặt phẳng (ABCD) và (A’B’C’D’) bằng
A. 45 ° .
B. 60 ° .
C. 0 ° .
D. 90 ° .
Cho hình lập phương ABCD.A’B’C’D’. Tính số đo góc giữa hai mặt phẳng (BA’C) và (DA’C). Tính số đo góc giữa hai mặt phẳng (BA’C) và (DA’C)
A. 60°
B. 135°
C. 150°
D. 90°
Cho hình lập phương
ABCD
.
A
’
B
’
C
’
D
’
có cạnh bằng a. Số đo của góc giữa hai mặt phẳng (BA’C) và (DA’C) là A.
90
o
B.
60
o
C.
30
o
D.
45
o
Đọc tiếp
Cho hình lập phương ABCD . A ’ B ’ C ’ D ’ có cạnh bằng a. Số đo của góc giữa hai mặt phẳng (BA’C) và (DA’C) là
A. 90 o
B. 60 o
C. 30 o
D. 45 o
Cho hình lập phương ABCD.A’B’C’D’, gọi
φ
là góc giữa hai mặt phẳng (A’BD) và (ABC). Tính
tan
φ
A.
tan
φ
1
2
B.
tan
φ
2
C.
tan
φ
2
3
D.
tan...
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’, gọi φ là góc giữa hai mặt phẳng (A’BD) và (ABC). Tính tan φ
A. tan φ = 1 2
B. tan φ = 2
C. tan φ = 2 3
D. tan φ = 3 2
Cho hình lập phương ABCD.A’B’C’D’. Tính góc giữa mặt phẳng (ABCD) và (ACC’A’).
A. 45 ο
B. 60 ο
C. 30 ∘
D. 90 ∘
