Các câu hỏi tương tự
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB1,
B
C
a
2
,
A
A
a
3
. Gọi α là góc giữa hai mặt phẳng (ACD’) và (ABCD) (tham khảo hình vẽ). Giá trị tanα bằng A.
3
2
2
B.
2
3
C. 2 D.
2...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB=1, B C = a 2 , A A ' = a 3 . Gọi α là góc giữa hai mặt phẳng (ACD’) và (ABCD) (tham khảo hình vẽ). Giá trị tanα bằng
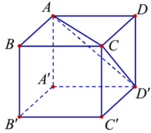
A. 3 2 2
B. 2 3
C. 2
D. 2 6 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy và
S
A
2
a
.
Góc giữa đường thẳng SC và mặt phẳng (ABCD) là
α
.
Khi đó
t
a
n
α
bằng: A.
2
B.
2
3
C. 2 D.
2
2
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy và S A = 2 a . Góc giữa đường thẳng SC và mặt phẳng (ABCD) là α . Khi đó t a n α bằng:
A. 2
B. 2 3
C. 2
D. 2 2
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có
A
B
a
;
B
C
a
2
;
A
A
a
3
Gọi
α
là góc giữa hai mặt phẳng (ACD’) và (ABCD) (tham khảo hình vẽ). Giá trị tanα bằng A.
2
6
3
B.
2...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có A B = a ; B C = a 2 ; A A ' = a 3 Gọi α là góc giữa hai mặt phẳng (ACD’) và (ABCD) (tham khảo hình vẽ). Giá trị tanα bằng
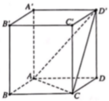
A. 2 6 3
B. 2 3
C. 2
D. 3 2 2
Cho hình lăng trụ đều ABC.ABC có tất cả các cạnh bằng a. Gọi M là trung điểm của AB và α là góc tạo bởi đường thẳng MC’ và mặt phẳng (ABC). Khi đó
tan
α
bằng A.
2
7
7
B.
3
2
C.
3
7
D.
2...
Đọc tiếp
Cho hình lăng trụ đều ABC.A'B'C' có tất cả các cạnh bằng a. Gọi M là trung điểm của AB và α là góc tạo bởi đường thẳng MC’ và mặt phẳng (ABC). Khi đó tan α bằng
A. 2 7 7
B. 3 2
C. 3 7
D. 2 3 3
Cho hình lăng trụ đều ABC.ABC có tất cả các cạnh bằng a. Gọi M là trung điểm của AB và α là góc tạo bởi đường thẳng MC’ và mặt phẳng (ABC). Khi đó tanα bằng A.
2
7
7
.
B.
3
2
.
C.
3
7
....
Đọc tiếp
Cho hình lăng trụ đều ABC.A'B'C' có tất cả các cạnh bằng a. Gọi M là trung điểm của AB và α là góc tạo bởi đường thẳng MC’ và mặt phẳng (ABC). Khi đó tanα bằng
A. 2 7 7 .
B. 3 2 .
C. 3 7 .
D. 2 3 3 .
Cho hình lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M là trung điểm của AB và
α
là góc tạo bởi đường thẳng MC’ và mặt phẳng (ABC). Khi đó
tan
α
bằng A.
2
7
7
.
B.
3
2
.
C.
3
7...
Đọc tiếp
Cho hình lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M là trung điểm của AB và α là góc tạo bởi đường thẳng MC’ và mặt phẳng (ABC). Khi đó tan α bằng
A. 2 7 7 .
B. 3 2 .
C. 3 7 .
D. 2 3 3 .
Cho hình chóp S.ACBD có đáy ABCD là hình vuông cạnh a các mặt bên (SAB).(SAD) cùng vuông góc với mặt phẳng đáy, SAa; góc giữa đường thẳng SC và mặt phẳng(SAB) bằng
α
. Khi đó
tan
α
nhận giá trị nào trong các giá trị sau: A.
tan
α
1
2
B.
tan
α
1
C.
tan
α
3
D. ...
Đọc tiếp
Cho hình chóp S.ACBD có đáy ABCD là hình vuông cạnh a các mặt bên (SAB).(SAD) cùng vuông góc với mặt phẳng đáy, SA=a; góc giữa đường thẳng SC và mặt phẳng(SAB) bằng α . Khi đó tan α nhận giá trị nào trong các giá trị sau:
A. tan α = 1 2
B. tan α = 1
C. tan α = 3
D. tan α = 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,
A
B
1
,
B
C
2
, mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi α là số đo của góc giữa hai mặt phẳng (SAB), (ABC). Khi đó tanα bằng A. 2 B.
3
2
C.
3
3
D. 1
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, A B = 1 , B C = 2 , mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi α là số đo của góc giữa hai mặt phẳng (SAB), (ABC). Khi đó tanα bằng
A. 2
B. 3 2
C. 3 3
D. 1
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, SA vuông góc với đáy (ABCD). Góc giữa đường thẳng SC và mặt phẳng (SAB) bằng
α
với
tan
α
10
5
. Tính góc giữa đường thẳng SO và mặt phẳng (ABCD). A.
60
°
B.
69
,
3
°
C.
90
°
D.
45
°
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, SA vuông góc với đáy (ABCD). Góc giữa đường thẳng SC và mặt phẳng (SAB) bằng α với tan α = 10 5 . Tính góc giữa đường thẳng SO và mặt phẳng (ABCD).
A. 60 °
B. 69 , 3 °
C. 90 °
D. 45 °