Đáp án D
Ta có MC là hình chiếu vuông góc của MC’ lên mặt phẳng (ABC)
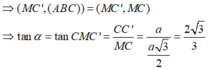
Đáp án D
Ta có MC là hình chiếu vuông góc của MC’ lên mặt phẳng (ABC)
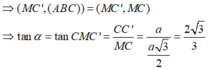
Cho hình lăng trụ đều ABC.A'B'C' có tất cả các cạnh bằng a. Gọi M là trung điểm của AB và α là góc tạo bởi đường thẳng MC’ và mặt phẳng (ABC). Khi đó tanα bằng
A. 2 7 7 .
B. 3 2 .
C. 3 7 .
D. 2 3 3 .
Cho hình lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M là trung điểm của AB và α là góc tạo bởi đường thẳng MC’ và mặt phẳng (ABC). Khi đó tan α bằng
A. 2 7 7 .
B. 3 2 .
C. 3 7 .
D. 2 3 3 .
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của các cạnh BC và SA, α là góc tạo bởi đường thẳng EM và mặt phẳng S B D , tan α bằng
A. 2
B. 3
C. 2
D. 1
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của BC, SA, α là góc tạo bởi đường thẳng EM và mặt phẳng (SBD), tan α bằng:
A. 1
B. 2
C. 2
D. 3
Cho hình lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi α là số đo của góc hợp bởi hai mặt phẳng (AB’C) và (BCC’B’). Khi đó cosα bằng
A. 7 7
B. 2 7 7
C. 10 4
D. 3 4
Cho lăng trụ ABC.A’B’C’có AB = 2a, BC = 2a, góc A’B’C’ = 120 0 . Hình chiếu vuông góc của A trên mặt phẳng (A’B’C’) trung với điểm của A’B’. Góc giữa đường thẳng AC’ và mặt phẳng (A’B’C’) bằng 60 0 . Gọi α là góc giữa hai mặt phẳng (BCC’B’) và (ABC). Khi đó, tan α có giá trị là:
A. 21
B. 2 2
C. 21 2
D. 2 21
Cho hình lăng trụ A B C . A ' B ' C ' có đáy ABC là tam giác đều cạnh a, tam giác A' BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC), M là trung điểm cạnh CC'. Tính cosin góc α giữa hai đường thẳng AA' và BM.
A. cos α = 2 22 11
B. cos α = 11 11
C. cos α = 33 11
D. cos α = 22 11
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a; tam giác A’BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABC) M là trung điểm của cạnh CC’. Tính cosin góc α là góc giữa hai đường thẳng AA’ và BM
A. cos α = 2 22 11
B. cos α = 11 11
C. cos α = 33 11
D. cos α = 22 11
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của các cạnh BC và SA, α là góc tạo bởi đường thẳng EM và mặt phẳng (SBD), tan α bằng:
A. 2 .
B. 3
C. 2
D. 1