Các câu hỏi tương tự
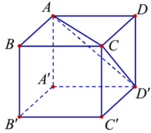
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có
A
B
a
;
B
C
a
2
;
A
A
a
3
Gọi
α
là góc giữa hai mặt phẳng (ACD’) và (ABCD) (tham khảo hình vẽ). Giá trị tanα bằng A.
2
6
3
B.
2...
Đọc tiếp
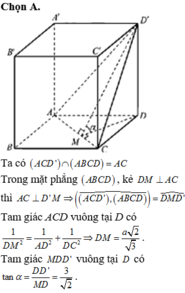
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có A B = a ; B C = a 2 ; A A ' = a 3 Gọi α là góc giữa hai mặt phẳng (ACD’) và (ABCD) (tham khảo hình vẽ). Giá trị tanα bằng
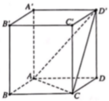
A. 2 6 3
B. 2 3
C. 2
D. 3 2 2
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB a,
BC
a
2
,
AA
a
3
. Gọi a là góc giữa 2 mặt phẳng (ACD’) và (ABCD) (tham khảo hình vẽ). Giá trị tana bằng: A. 2 B.
2
6
3
C.
3
2...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = a 2 , AA ' = a 3 . Gọi a là góc giữa 2 mặt phẳng (ACD’) và (ABCD) (tham khảo hình vẽ). Giá trị tana bằng:
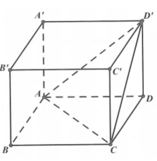
A. 2
B. 2 6 3
C. 3 2 2
D. 2 3
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB1,BC2,AA3. Côsin góc giữa hai mặt phẳng (ACD′) và (BCD′A′) bằng A.
2
10
7
B.
3
7
C.
3
35
35
D.
910
35
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=1,BC=2,AA'=3. Côsin góc giữa hai mặt phẳng (ACD′) và (BCD′A′) bằng
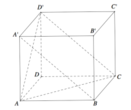
A. 2 10 7
B. 3 7
C. 3 35 35
D. 910 35
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB1,BC2,AA
3
. Côsin góc giữa hai mặt phẳng (ACD′) và (BCD′A′) bằng A.
57
19
B.
4
19
19
C.
6
4
D.
10...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=1,BC=2,AA'= 3 . Côsin góc giữa hai mặt phẳng (ACD′) và (BCD′A′) bằng
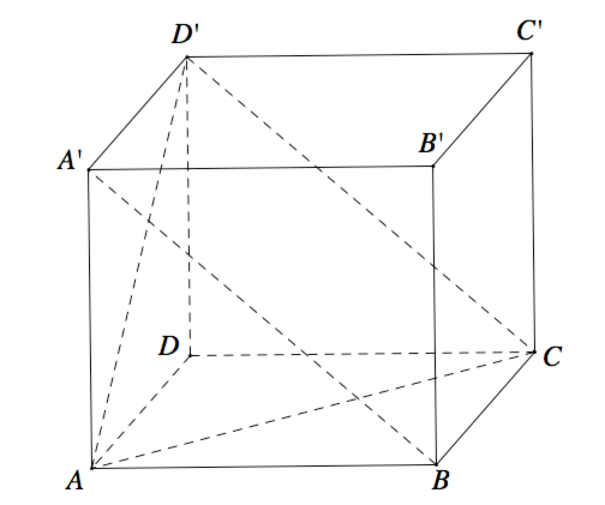
A. 57 19
B. 4 19 19
C. 6 4
D. 10 4
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có các cạnh
A
B
2
,
A
D
3
,
A
A
4.
Góc giữa mặt phẳng (ABD) và (ACD) là
α
. Tính giá trị gần đúng của góc
α
?
A.
42
,
5
°
B.
38
,
1
°
C.
53
,...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có các cạnh A B = 2 , A D = 3 , A A ' = 4. Góc giữa mặt phẳng (AB'D') và (A'C'D) là α . Tính giá trị gần đúng của góc α ?
A. 42 , 5 °
B. 38 , 1 °
C. 53 , 4 °
D. 61 , 6 °
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
, biết
A
C
3
,
C
D
2,
D
A
5
. Góc giữa hai mặt phẳng...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' , biết A C = 3 , C D ' = 2, D ' A = 5 . Góc giữa hai mặt phẳng A C D ' và A ' B ' C ' D ' là α, tan α bằng
A. 3 2 2
B. 2 6 3
C. 2 3
D. 30 6
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B;
A
B
B
C
1
,
A
D
2.
Các mặt chéo
S
A
C
và
S
B
D
cùng vuông góc với mặt đáy
A
B
C
D...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B; A B = B C = 1 , A D = 2. Các mặt chéo S A C và S B D cùng vuông góc với mặt đáy A B C D . Biết góc giữa hai mặt phẳng S A B và A B C D bằng 60 0 (tham khảo hình vẽ bên). Khoảng cách từ điểm D đến mặt phẳng S A B là
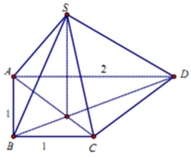
A. 2 3 3
B. 3
C. 2 3
D. 3 3
Cho lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật với
A
B
6
,
A
D
3
,
A
C
3
và mặt phẳng
A
A
C
C
vuông góc với mặt đáy. Biết hai mặt phẳng tạo với nhau góc thỏa mãn...
Đọc tiếp
Cho lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật với A B = 6 , A D = 3 , A ' C = 3 và mặt phẳng A A ' C ' C vuông góc với mặt đáy. Biết hai mặt phẳng tạo với nhau góc thỏa mãn tan α = 3 4 . Thể tích khối lăng trụ ABCD.A’B’C’D’ bằng
A. V = 8
B. V = 12
C. V = 10
D. V = 6
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB1,BC2,AA3.. Tính sin của góc giữa đường thẳng A′C và mặt phẳng (A′BD). A.
5
91
49
B.
3
14
49
C.
9
14
98
D.
11
70...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=1,BC=2,AA'=3.. Tính sin của góc giữa đường thẳng A′C và mặt phẳng (A′BD).
A. 5 91 49
B. 3 14 49
C. 9 14 98
D. 11 70 98