Các câu hỏi tương tự
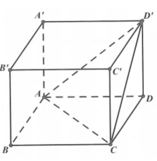
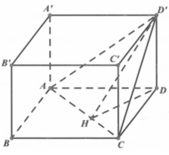
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có
A
B
a
;
B
C
a
2
;
A
A
a
3
Gọi
α
là góc giữa hai mặt phẳng (ACD’) và (ABCD) (tham khảo hình vẽ). Giá trị tanα bằng A.
2
6
3
B.
2...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có A B = a ; B C = a 2 ; A A ' = a 3 Gọi α là góc giữa hai mặt phẳng (ACD’) và (ABCD) (tham khảo hình vẽ). Giá trị tanα bằng
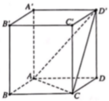
A. 2 6 3
B. 2 3
C. 2
D. 3 2 2
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB1,
B
C
a
2
,
A
A
a
3
. Gọi α là góc giữa hai mặt phẳng (ACD’) và (ABCD) (tham khảo hình vẽ). Giá trị tanα bằng A.
3
2
2
B.
2
3
C. 2 D.
2...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB=1, B C = a 2 , A A ' = a 3 . Gọi α là góc giữa hai mặt phẳng (ACD’) và (ABCD) (tham khảo hình vẽ). Giá trị tanα bằng
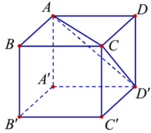
A. 3 2 2
B. 2 3
C. 2
D. 2 6 3
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB1,BC2,AA3. Côsin góc giữa hai mặt phẳng (ACD′) và (BCD′A′) bằng A.
2
10
7
B.
3
7
C.
3
35
35
D.
910
35
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=1,BC=2,AA'=3. Côsin góc giữa hai mặt phẳng (ACD′) và (BCD′A′) bằng
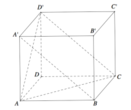
A. 2 10 7
B. 3 7
C. 3 35 35
D. 910 35
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB1,BC2,AA
3
. Côsin góc giữa hai mặt phẳng (ACD′) và (BCD′A′) bằng A.
57
19
B.
4
19
19
C.
6
4
D.
10...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=1,BC=2,AA'= 3 . Côsin góc giữa hai mặt phẳng (ACD′) và (BCD′A′) bằng
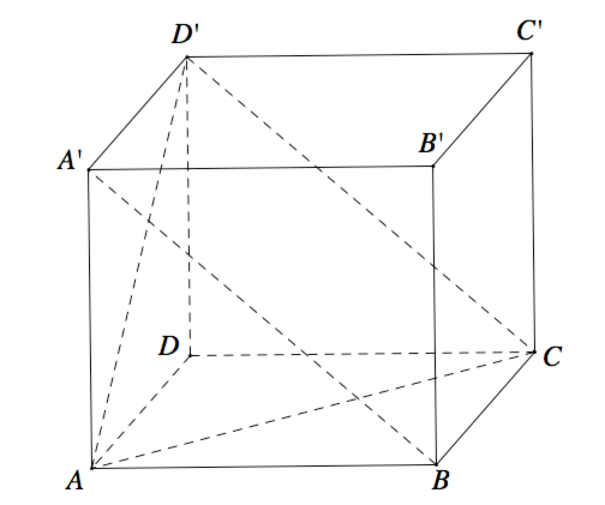
A. 57 19
B. 4 19 19
C. 6 4
D. 10 4
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có các cạnh
A
B
2
,
A
D
3
,
A
A
4.
Góc giữa mặt phẳng (ABD) và (ACD) là
α
. Tính giá trị gần đúng của góc
α
?
A.
42
,
5
°
B.
38
,
1
°
C.
53
,...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có các cạnh A B = 2 , A D = 3 , A A ' = 4. Góc giữa mặt phẳng (AB'D') và (A'C'D) là α . Tính giá trị gần đúng của góc α ?
A. 42 , 5 °
B. 38 , 1 °
C. 53 , 4 °
D. 61 , 6 °
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB1,BC2,AA3.. Tính sin của góc giữa đường thẳng A′C và mặt phẳng (A′BD). A.
5
91
49
B.
3
14
49
C.
9
14
98
D.
11
70...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=1,BC=2,AA'=3.. Tính sin của góc giữa đường thẳng A′C và mặt phẳng (A′BD).
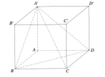
A. 5 91 49
B. 3 14 49
C. 9 14 98
D. 11 70 98
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B;
A
B
B
C
1
,
A
D
2.
Các mặt chéo
S
A
C
và
S
B
D
cùng vuông góc với mặt đáy
A
B
C
D...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B; A B = B C = 1 , A D = 2. Các mặt chéo S A C và S B D cùng vuông góc với mặt đáy A B C D . Biết góc giữa hai mặt phẳng S A B và A B C D bằng 60 0 (tham khảo hình vẽ bên). Khoảng cách từ điểm D đến mặt phẳng S A B là
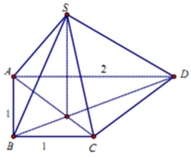
A. 2 3 3
B. 3
C. 2 3
D. 3 3
Cho hình lăng trụ tam giác đều ABC.A B Cvới AB2
3
,AA2 (tham khảo hình vẽ bên). Tang góc giữa đường thẳng AB’ và mặt phẳng (BCC B ) bằng A.
3
B.
1
3
C.
3
7
D.
7
3
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A' B' C'với AB=2 3 ,AA'=2 (tham khảo hình vẽ bên). Tang góc giữa đường thẳng AB’ và mặt phẳng (BCC' B' ) bằng
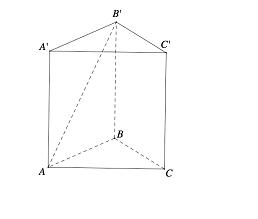
A. 3
B. 1 3
C. 3 7
D. 7 3
Cho hình hộp chữ nhật ABCD.ABCD có AB4,AD5,AA6. Gọi M , N , P lần luợt là trung điểm các cạnh AD,CD và DD (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (ABD) và (MNP) bằng A.
181
469
B.
120
13
469
C.
19
469
D.
60
61
469
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=4,AD=5,AA'=6. Gọi M , N , P lần luợt là trung điểm các cạnh A'D',C'D' và DD' (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (AB'D') và (MNP) bằng
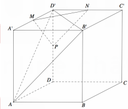
A. 181 469
B. 120 13 469
C. 19 469
D. 60 61 469