Đáp án C
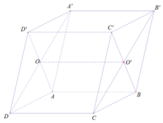
Ta có: C’B ∩ CB’ = O '
⇒ O’ là điểm chung của (A’B’CD) và (ABC’D’)
A’D ∩ AD’ = O
⇒ O là điểm chung của (A’B’CD) và (ABC’D’)
⇒ OO’ là giao tuyến cần tìm
Đáp án C

Ta có: C’B ∩ CB’ = O '
⇒ O’ là điểm chung của (A’B’CD) và (ABC’D’)
A’D ∩ AD’ = O
⇒ O là điểm chung của (A’B’CD) và (ABC’D’)
⇒ OO’ là giao tuyến cần tìm
Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt .Gọi O là giao điểm của AC và BD, O’ là giao điểm của AE và BF.
a) Chứng minh rằng OO’ song song với hai mặt phẳng (ADF) và (BCE)
b) Gọi M và N lần lượt là trọng tâm của các tam giác ABDvà ABE. Chứng minh rằng .
Cho hình hộp ABCD.A’B’C’D’.
a) Chứng minh rằng hai mặt phẳng (BDA’) và (B’D’C) song song với nhau.
b) Chứng minh rằng đường chéo AC’ đi qua trọng tâm G1 và G2 lần lượt của hai tam giác BDA’ và B’D’C.
c) Chứng minh G1 và G2 chia đoạn AC’ thành ba phần bằng nhau.
d) Gọi O và I lần lượt là tâm các hình bình hành ABCD và AA’C’C. Xác định thiết diện của mặt phẳng (A’IO) với hình hộp đã cho.
cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật tâm O. Gọi H,K lần lượt là trung điểm SA,SB
a) tìm giao tuyến của hai mặt phẳng (SBD) và (SAC)
b) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
c) tìm giao tuyến của 2 mặt phẳng (SAD) và (SBC)
d) tìm giao tuyến của 2 mặt phẳng (HKCD) và (ABCD)
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai mặt phẳng (A’B’CD) và (ABC’D’) bằng
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M là một điểm trên cạnh SC và (a) là mặt phẳng chứa AM và song song với BD. a. Tìm giao tuyến của hai mặt phăng (SAC) và (SBD) ? b. Tìm các giao điểm E, F của mặt phẳng (a) lần lượt với các cạnh SB, SD.
cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật tâm O. Gọi H,K lần lượt là trung điểm SA,SB
a) tìm giao tuyến của 2 mặt phẳng (SBD) và (SAC)
b) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
c) tìm giao tuyến của 2 mặt phẳng (SAD) và (SBC)
d) tìm giao tuyến của 2 mặt phẳng (HKCD) và (ABCD)
cho hình chóp S.ABCD, đáy ABCD là vuông tâm I. Gọi M,N lần lượt là trung điểm SB,SC
a) tìm giao tuyến của hai mặt phẳng (SBD) và (SAC)
b) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
c) tìm giao tuyến của 2 mặt phẳng (SAD) và (SBC)
d) tìm giao tuyến của 2 mặt phẳng (MNA) và (ABCD)
Cho bốn điểm A, B, C và D không đồng phẳng. Gọi I, K lần lượt là trung điểm của AD và BC.
a) Tìm giao tuyến của hai mặt phẳng (IBC) và (KAD).
b) Gọi M và N là hai điểm lần lượt lấy trên hai đoạn thẳng AB và AC. Tìm giao tuyến của hai mặt phẳng (IBC) và (DMN).
Cho hình lập phương ABCD.A’B’C’D’ có độ dài cạnh bằng 10. Tính khoảng cách giữa hai mặt phẳng (ADD’A’) và (BCC’B’)
A. 10
B. 100
C. 10
D. 5