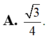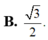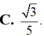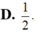Các câu hỏi tương tự
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 2. Tính khoảng cách giữa hai mặt phẳng (A’B’D’) và (BC’D)
A
.
3
3
B
.
3
C
.
3
2
D
.
2
3
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 2. Tính khoảng cách giữa hai mặt phẳng (A’B’D’) và (BC’D)
A . 3 3
B . 3
C . 3 2
D . 2 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 10. Cạnh bên SA vuông góc với mặt phẳng (ABCD) và SC = 10√5. Gọi M,N lần lulư là trung điểm của SA và CD. Tính khoảng cách d giữa BD và MN.
A. d=3√5
B. d=√5
C. d=5
D. d=10
Cho hình hộp thoi ABCD.A’B’C’D’ có các cạnh đều bằng a và
B
A
D
^
B
A
A
^
D
A
A
^
60
°
. Tính khoảng cách giữa hai mặt phẳng đáy (ABCD) và (A’B’C’D’). A. ...
Đọc tiếp
Cho hình hộp thoi ABCD.A’B’C’D’ có các cạnh đều bằng a và B A D ^ = B A A ' ^ = D A A ' ^ = 60 ° . Tính khoảng cách giữa hai mặt phẳng đáy (ABCD) và (A’B’C’D’).
A. a 5 5
B. a 6 3
C. a 10 5
D. a 3 3
Cho hình hộp ABCD.A’B’C’D’. Gọi O, O’ lần lượt là tâm của hai mặt ADD’A’ và BCC’B’. Tìm giao tuyến của hai mặt (ABC’D’) và (A’B’CD)?
A. BD’
B. A’C
C. OO’
D. AC.
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khoảng cách giữa hai đường thẳng BD và CB’ bằng A.
a
6
3
B.
2
a
3
3
C.
a
2
2
D.
a
3...
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khoảng cách giữa hai đường thẳng BD và CB’ bằng
A. a 6 3
B. 2 a 3 3
C. a 2 2
D. a 3 3
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a (hình vẽ bên). Khoảng cách giữa hai đường thẳng BD và A’C’ là:
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a (hình vẽ bên). Khoảng cách giữa hai đường thẳng BD và A’C’ là:
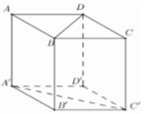
![]()
![]()
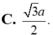
![]()
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng BD và AC’ là A.
3
a
B.
a
A.
3
2
a
A.
2
a
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng BD và AC’ là
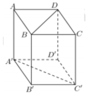
A. 3 a
B. a
A. 3 2 a
A. 2 a
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a, gọi α là góc giữa đường thẳng A’B và mặt phẳng (BB’D’D). Tính sin α. A.
3
4
B.
3
2
C.
3
5
D.
1
2
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a, gọi α là góc giữa đường thẳng A’B và mặt phẳng (BB’D’D). Tính sin α.
A. 3 4
B. 3 2
C. 3 5
D. 1 2
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a, gọi
α
là góc giữa đường thẳng AB’ và mặt phẳng (BB’D’D) Tính sin
α
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a, gọi α là góc giữa đường thẳng AB’ và mặt phẳng (BB’D’D) Tính sin α