Cho hàm số 1000 x - 1 + x - 2 x 2 - 1 k h i x > 1 2 a x k h i x ≤ 1 .Tìm a để hàm số liên tục tại x=1?
A. 3 log 10 2
B. 3 ln 10 2
C.Đáp án khác
D. 3 ln 10 + 1 4
Cho hàm số y = f ( x ) có đạo hàm trên ℝ . Xét các hàm số g ( x ) = f x − f 2 x và h ( x ) = f ( x ) − f ( 4 x ) . Biết rằng g ' ( 1 ) = 18 và g ' ( 2 ) = 1000 . Tính h ' ( 1 ) :
A. − 2018
.
B. 2018
C. 2020
D. − 2020
Giúp pé bài này zs mấy ACE ey
Cho hàm số y = f (x) = ax + b
Biết f (1) = f (2) ; f (5)\(\ge\)f (6) ; f (2000) = 1000
Tính f (2016)
1. Cho hàm số y =f(x) có đạo hàm f'(x) = (x^2 -1)(x-2)^2(x-3) . Hàm số đồng biến ; nghịch biến trên khoảng nào? 2. Cho hàm số y = x^4 -2x^2 . Hàm số đồng biến ; nghịch biến trên khoảng nào?
1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = x ( x + 1 ) ( 1 - 2 x ) 3 , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là
A. 3
B. 1
C. 5
D. 2
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = x 2 ( x - 1 ) ( x - 2 ) ( 3 x - 1 ) , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho bằng
A. 2
B. 1
C. 3
D. 4
Cho hàm số y=f(x) có đạo hàm f ’ ( x ) = x 2 ( x - 1 ) ( x 2 - 1 ) 3 . Số điểm cực trị của hàm số đã cho là
A. 2
B. 1
C. 8
D. 3
Chọn đáp án B
Phương pháp
Số điểm cực trị của hàm số y=f(x) là số nghiệm bội lẻ của phương trình f’(x)=0.
Cách giải
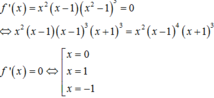
Tuy nhiên x=0 là nghiệm bội 2, x=1 là nghiệm bội 4 của phương trình f’(x)=0, do đó chúng không là cực trị của hàm số. Vậy hàm số có duy nhất 1 điểm cực trị x=-1.
Chú ý: HS nên phân tích đa thức f’(x) thành nhân tử triệt để trước khi xác định nghiệm, tránh sai lầm khi kết luận x=1 cũng là cực trị của hàm số.
Cho hàm số f (x) có đạo hàm f'(x) = x(x-1) x + 2 3 , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là
A. 3
B. 2
C. 5
D. 1
Đáp án A
Phương pháp:
Giải phương trình f'(x) = 0 rồi lập bảng biến thiên để xác định các điểm cực trị
Hoặc ta xét trong các nghiệm của phương trình f'(x) = 0thì qua nghiệm bậc lẻ f'(x) sẽ đổi dấu, qua nghiệm bội bậc chẵn thì f'(x) không đổi dấu. Hay các nghiệm bội lẻ là các điểm cực trị của hàm số đã cho.
Cách giải:
Ta có ![]()
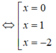
và các nghiệm này đều là nghiệm bội bậc lẻ nên hàm số đã cho có ba điểm cực trị
Cho hàm số f(x) có đạo hàm f ’ ( x ) = x ( x - 1 ) ( x + 2 ) 2 . Số điểm cực trị của hàm số đã cho là:
A. 2
B. 1
C. 4
D. 3
Cho hàm số f ( x ) = x 3 - 2 x 2 + x + 1 - 1 x - 1 k h i x ≠ 1 0 k h i x = 1 . Tính đạo hàm của hàm số
A. 1 3
B. 1 5
C. 1 2
D. 1 4
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = x ( x - 1 ) ( x + 2 ) 3 , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là:
A. 2
B. 3
C. 5
D. 1