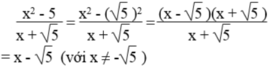Rút gọn các phân thức: 9 - x + 5 2 x 2 + 4 x + 4

Những câu hỏi liên quan
Rút gọn các phân thức:
x
2
-
5
x
+
5
v
ớ
i
x
≠...
Đọc tiếp
Rút gọn các phân thức: x 2 - 5 x + 5 v ớ i x ≠ - 5
cho phân thức: \(\dfrac{x^2-6x+9}{x^2-3x}\)
a)tìm điều kiện của x để giá trị phân thức được xác định
b)rút gọn phân thức
c)tính giá trị của phân thức khi x=5?
`a,`
\(x^2-3x\ne0\)
`<=>x(x-3)`\(\ne0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne0\\x-3\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne0\\x\ne3\end{matrix}\right.\)
`b,`
đặt `A=(x^2-6x+9)/(x^2-3x)`
`A= ((x-3)^2)/(x(x-3))`
`A= (x-3)/x`
`c, `
để `x=5`
`=> A= (x -3)/x=(5-3)/5= 2/5`
Đúng 1
Bình luận (0)
a/ ĐKXĐ: \(x^2-3x\ne0\) \(\Leftrightarrow\) x\(\ne\)0,x\(\ne\)3
b/ \(\dfrac{x^2-6x+9}{x^2-3x}=\dfrac{\left(x-3\right)^2}{x\left(x-3\right)}=\dfrac{x-3}{x}\)
c/ x= 5 => \(\dfrac{x-3}{x}=\dfrac{5-3}{5}=\dfrac{2}{5}\)
Đúng 3
Bình luận (0)
câu 3 phân thức nghịch đảo của phân thức 2/x-4v(với x≠4)
câu 4 phân thức 2/ x-3 không có nghĩa khi
câu 5 rút gọn phân thức x-3/ x^2-9 ( với x≠ cộng trừ 3) ta được kết quả
Câu 4: Không có nghĩa khi x-3=0
=>x=3
Câu 5:
\(A=\dfrac{x-3}{\left(x-3\right)\left(x+3\right)}=\dfrac{1}{x+3}\)
Đúng 1
Bình luận (0)
rút gọn phân thức: 2x-5/2x2-9x+9 - x-7/2x2+x-6
rút gọn phân thức x^2-9/x+3
\(=\dfrac{\left(x-3\right)\left(x+3\right)}{x+3}=x-3\)
Đúng 0
Bình luận (0)
1. Rút gọn phân thức \(\dfrac{\left(x+y\right)^2}{x^2-y^2}=\) ta được kết quả là:
2. Rút gọn phân thức \(\dfrac{x^2-3x}{x^2-9}=\)
giúp mình với nhé mình đang cần gấp ạ
1. = \(\dfrac{x+y}{x-y}\)
2. = \(\dfrac{x}{x+3}\)
Đúng 0
Bình luận (0)
Cho phân thức: x2-9/x+3
a) Tìm điều kiện của x để giá trị của phân thức xác định.
b)Rút gọn phân thức.
a: ĐKXĐ: x<>-3
b: \(=\dfrac{\left(x-3\right)\left(x+3\right)}{x+3}=x-3\)
Đúng 1
Bình luận (0)
a) ĐKXĐ: \(x\ne-3\)
b) \(\dfrac{x^2-9}{x+3}=\dfrac{\left(x-3\right)\left(x+3\right)}{x+3}=x-3\)
Đúng 0
Bình luận (0)
rút gọn phân thức: x^2-3x phần x^2-6x+9
\(\dfrac{x^2-3x}{x^2-6x+9}=\dfrac{x\left(x-3\right)}{\left(x-3\right)^2}=\dfrac{x}{x-3}.\)
ĐKXĐ: \(x\ne3.\)
Đúng 0
Bình luận (0)
\(=\dfrac{\left(x-3\right)\cdot x}{\left(x-3\right)^2}=\dfrac{x}{x-3}\)
Đúng 0
Bình luận (0)
Bài 4 (3,0 điểm) Rút gọn các phân thức sau: B = (x + y)² - z²/x + y + z
c) C = x² - 6x + 5/x² - 2x + 1
b: \(B=\dfrac{\left(x+y\right)^2-z^2}{x+y+z}\)
\(=\dfrac{\left(x+y-z\right)\left(x+y+z\right)}{x+y+z}\)
=x+y-z
c:
ĐKXĐ: x<>1
\(C=\dfrac{x^2-6x+5}{x^2-2x+1}\)
\(=\dfrac{\left(x-1\right)\left(x-5\right)}{\left(x-1\right)^2}\)
\(=\dfrac{x-5}{x-1}\)
Đúng 0
Bình luận (0)