Một chỉnh hợp chập 2 của tập A = 1 , 2 , 3 , 4 , 5 là:
A. A 5 2
B. C 5 2
C. ( 2 , 5 )
D. 2 , 5
Những câu hỏi liên quan
Một chỉnh hợp chập 2 của tập
A
1
,
2
,
3
,
4
,
5
là: A.
A
5
2
B.
C
5
2
C.
2
;
5
D. ...
Đọc tiếp
Một chỉnh hợp chập 2 của tập A = 1 , 2 , 3 , 4 , 5 là:
A. A 5 2
B. C 5 2
C. 2 ; 5
D. 2 ; 5
Một chỉnh hợp chập 2 của tập A={1,2,3,4,5} là:
A. A 5 2 .
B. C 5 2 .
C. (2,5).
D. {2,5}.
Cho tập hợp A = {a, b, c, d, e}.
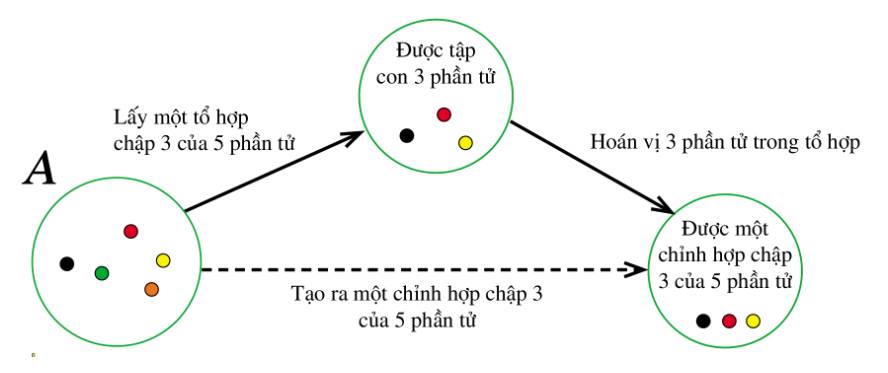
a) Nêu cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A.
b) Nêu cách lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A.
c) So sánh cách lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A với cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A.
a) Cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A là: Chọn bất kỳ 3 trong 5 phần tử thuộc A ví dụ như \(\left\{ {a;b;c} \right\}\)
b) Cách lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A là: Chọn bất kỳ 3 trong 5 phần tử thuộc A rồi sắp xếp theo một thứ tự nào ví dụ như ta chọn 3 phần tử a,b,c rồi sắp xếp theo thứ tự ngược của bảng chữ cái \(\left\{ {c;b;a} \right\}\)
c) So sánh: Mỗi tổ hợp chập 3 của 5 phần tử sinh ra 3! chỉnh hợp chập 3 của 5 phần tử vì có 3! hoán vị của 3 phần tử. Vì thế, số chỉnh hợp chập 3 của 5 phần tử nhiều gấp 3! lần số tổ hợp chập 3 của 5 phần tử.
Đúng 0
Bình luận (0)
Cho tập A có n phần tửv( n > 2 ) k là một số nguyên 0<k<n Số chỉnh hợp chập k của n phần tử là
Tìm số các chỉnh hợp chập k của một tập hợp gồm n phần tử
1
≤
k
≤
n
Đọc tiếp
Tìm số các chỉnh hợp chập k của một tập hợp gồm n phần tử 1 ≤ k ≤ n
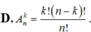
Số chỉnh hợp chập 6 của một tập hợp có 9 phần tử là:
A. 9!/(3!.6!).
B. 6!/3!.
C. 9!/6!.
D. 9!/3!.
Số chỉnh hợp chập 6 của một tập hợp có 9 phần tử là: A.
9
!
3
!
.
6
!
. B.
6
!
3
!
.
C. ...
Đọc tiếp
Số chỉnh hợp chập 6 của một tập hợp có 9 phần tử là:
A. 9 ! 3 ! . 6 ! .
B. 6 ! 3 ! .
C. 9 ! 6 ! .
D. 9 ! 3 ! .
Công thức tính số các chỉnh hợp chập k của một tập có n phần tử 1 ≤ k ≤ n là
A
.
C
n
k
n
!
(
n
-
k
)
!
B
.
C
n
k
...
Đọc tiếp
Công thức tính số các chỉnh hợp chập k của một tập có n phần tử 1 ≤ k ≤ n là
A . C n k = n ! ( n - k ) !
B . C n k = n ! k ! ( n - k ) !
C . A n k = n ! ( n - k ) !
D . A n k = n ! k ! ( n - k ) !
Số các chỉnh hợp chập k của một tập hợp gồm n phần tử (với k,n
∈
ℕ
*
,
k
≤
n
).
A
.
k
!
(
k
-
n
)
!
B
.
C
n...
Đọc tiếp
Số các chỉnh hợp chập k của một tập hợp gồm n phần tử (với k,n ∈ ℕ * , k ≤ n ).
A . k ! ( k - n ) !
B . C n k . k ! .
C . C n k . ( n - k ) ! .
D . k ! ( n - k ) ! n !
Chọn B
Ta có số chỉnh hợp chập k của một tập hợp gồm n phần tử là: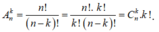 
.
Đúng 0
Bình luận (0)