Cho cấp số cộng u n có các số hạng đầu lần lượt là 5; 9; 13; 17; .... Tìm số hạng tổng quát u n của cấp số cộng?
A. u n = 4 n + 1
B. u n = 5 n - 1
C. u n = 5 n + 1
D. u n = 4 n - 1
Những câu hỏi liên quan
Cho cấp số cộng (un) có các số hạng đầu lần lượt là 5; 9; 13; 17;..... Tìm số hạng tổng quát un của cấp số cộng. A.
u
n
5
n
+
1.
B.
u
n
5
n
−
1.
C.
u
n
4
n
+
1.
D.
u
n
4
n...
Đọc tiếp
Cho cấp số cộng (un) có các số hạng đầu lần lượt là 5; 9; 13; 17;..... Tìm số hạng tổng quát un của cấp số cộng.
A. u n = 5 n + 1.
B. u n = 5 n − 1.
C. u n = 4 n + 1.
D. u n = 4 n − 1.
Các số 5; 9; 13; 17..... theo thứ tự đó lập thành cấp số cộng ( u n ) nên
u 1 = 5 d = u 2 − u 1 = 4 → C T T Q u n = u 1 + n − 1 d = 5 + 4 n − 1 = 4 n + 1
Chọn đáp án C.
Đúng 0
Bình luận (0)
Cho cấp số cộng
u
n
có các số hạng đầu lần lượt là 5; 9; 13; 17; .... Tìm số hạng tổng quát
u
n
của cấp số cộng? A.
u
n
4
n
+
1
B.
u
n
5
n
-
1
C.
u
n...
Đọc tiếp
Cho cấp số cộng u n có các số hạng đầu lần lượt là 5; 9; 13; 17; .... Tìm số hạng tổng quát u n của cấp số cộng?
A. u n = 4 n + 1
B. u n = 5 n - 1
C. u n = 5 n + 1
D. u n = 4 n - 1
Cho cấp số cộng
u
n
có các số hạng đầu lần lượt là 5; 9; 13; 17; … Tìm công thức số hạng tổng quát
u
n
của cấp số cộng? A.
u
n
5
n
-
1
B.
u
n
5
n
+
1
C. ...
Đọc tiếp
Cho cấp số cộng u n có các số hạng đầu lần lượt là 5; 9; 13; 17; … Tìm công thức số hạng tổng quát u n của cấp số cộng?
A. u n = 5 n - 1
B. u n = 5 n + 1
C. u n = 4 n - 1
D. u n = 4 n + 1
Cho cấp số cộng (un) có các số hạng đầu lần lượt là 5; 9; 13; 17; … Tìm công thức số hạng tổng quát un của cấp số cộng? A.
u
n
5
n
-
1
B.
u
n
5...
Đọc tiếp
Cho cấp số cộng (un) có các số hạng đầu lần lượt là 5; 9; 13; 17; … Tìm công thức số hạng tổng quát un của cấp số cộng?
A. u n = 5 n - 1
B. u n = 5 n + 1
C. u n = 4 n - 1
D. u n = 4 n + 1
Chọn D
Ta có: u1 = 5 nên thay n = 1 vào 4 đáp án thấy chỉ có đáp án D đúng
Đúng 0
Bình luận (0)
Ba số phân biệt có tổng 217, là các số hạng liên tiếp của một cấp số nhân, theo thứ tự đó chúng lần lượt là số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Biết tổng của n số hạng đầu tiên của cấp số cộng là 820, khi đó n bằng
A. 21
B. 42
C. 20
D. 17
Chọn C
Gọi ba số đó lần lượt là x,y,z
Do ba số là các số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng nên ta có liên hệ: y = x + 7 d , z = x + 42 (với d là công sai của cấp số cộng)
Theo giả thiết ta có: x + y + z = x + x + 7 d + x + 42 d = 3 x + 49 d = 217
Mặt khác do x,y,z là các số hạng liên tiếp của một cấp số nhân nên
Đúng 0
Bình luận (0)
Ba số phân biệt có tổng 217, là các số hạng liên tiếp của một cấp số nhân, theo thứ tự đó chúng lần lượt là số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Biết tổng của n số hạng đầu tiên của cấp số cộng là 820, khi đó n bằng A. 21 B. 42 C.20 D. 17
Đọc tiếp
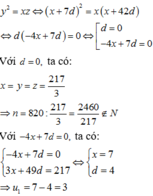
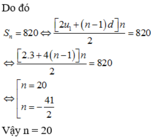
Ba số phân biệt có tổng 217, là các số hạng liên tiếp của một cấp số nhân, theo thứ tự đó chúng lần lượt là số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Biết tổng của n số hạng đầu tiên của cấp số cộng là 820, khi đó n bằng
A. 21
B. 42
C.20
D. 17
Cho cấp số cộng có tổng 10 số hạng đầu tiên và 100 số hạng đầu tiên lần lượt là 100 và 10. Khi đó tổng của 110 số hạng đầu tiên là:
A. 90
B. - 90
C. - 110
D. - 23
Cho cấp số cộng (un) có số hạng đầu là u = 1 và công sai d = 1. Tìm n sao cho tổng n số hạng đầu tiên của cấp số cộng đó bằng 3003
Xem chi tiết
Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77
Đúng 2
Bình luận (0)
Cho cấp số cộng left( {{u_n}} right) với số hạng đầu {u_1} và công sai dĐể tính tổng của n số hạng đầu {S_n} {u_1} + {u_2} + ldots + {u_{n - 1}} + {u_n}Hãy lần lượt thực hiện các yêu cầu sau:a) Biểu diễn mỗi số hạng trong tổng {S_n} theo số hạng đầu {u_n} và công sai db) Viết {S_n} theo thứ tự ngược lại: {S_n} {u_n} + {u_{n - 1}} + ldots + {u_2} + {u_1} và sử dụng kết quả ở phần a) để biểu diễn mỗi số hạng trong tổng này theo {u_1} và dc) Cộng từng vế...
Đọc tiếp
Cho cấp số cộng \(\left( {{u_n}} \right)\) với số hạng đầu \({u_1}\) và công sai d
Để tính tổng của n số hạng đầu
\({S_n} = {u_1} + {u_2} + \ldots + {u_{n - 1}} + {u_n}\)
Hãy lần lượt thực hiện các yêu cầu sau:
a) Biểu diễn mỗi số hạng trong tổng \({S_n}\) theo số hạng đầu \({u_n}\) và công sai d
b) Viết \({S_n}\) theo thứ tự ngược lại: \({S_n} = {u_n} + {u_{n - 1}} + \ldots + {u_2} + {u_1}\) và sử dụng kết quả ở phần a) để biểu diễn mỗi số hạng trong tổng này theo \({u_1}\) và d
c) Cộng từng vế hai đẳng thức nhận được ở a), b) để tính \({S_n}\)theo \({u_1}\) và d
a) \({u_2} = {u_1} + d\)
\({u_3} = {u_1} + 2d\)
…
\({u_{n - 1}} = {u_1} + \left( {n - 2} \right)d\)
\({u_n} = {u_1} + \left( {n - 1} \right)d\)
\({S_n} = {u_1} + {u_1} + 2d + \ldots + {u_1} + \left( {n - 2} \right)d + {u_1} + \left( {n - 1} \right)d\)
b) \({S_n} = {u_n} + {u_{n - 1}} + \ldots + {u_2} + {u_1} = {u_1} + \left( {n - 1} \right)d + {u_1} + \left( {n - 2} \right)d + \ldots + {u_1} + d + {u_1}\)
c) \(2{S_n} = \left( {{u_1} + {u_1} + d + \ldots + {u_1} + \left( {n - 1} \right)d} \right) + \left( {{u_1} + \left( {n - 1} \right)d + {u_1} + \left( {n - 2} \right)d + \ldots + {u_1}} \right)\).
\( \Rightarrow 2{S_n} = n.\left( {2{u_1} + \left( {n - 1} \right)d} \right)\)
\( \Rightarrow {S_n} = \frac{n}{2}\left( {2{u_1} + \left( {n - 1} \right)d} \right)\)
Đúng 0
Bình luận (0)