Cho hàm số ![]() có đồ thị là đường cong (C). Biết rằng tồn tại hai số thực
m
1
,
m
2
của tham số m để hai điểm cực trị của (C) và hai giao điểm của (C) với trục hoành tạo thành bốn đỉnh của một hình chữ nhật. Tính
có đồ thị là đường cong (C). Biết rằng tồn tại hai số thực
m
1
,
m
2
của tham số m để hai điểm cực trị của (C) và hai giao điểm của (C) với trục hoành tạo thành bốn đỉnh của một hình chữ nhật. Tính ![]() .
.
A. ![]()
B. ![]()
C. 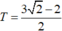
D. 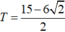




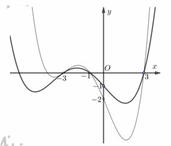
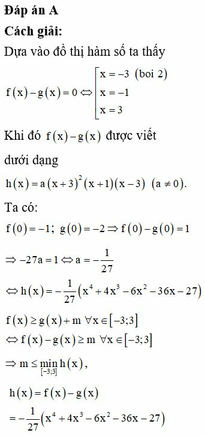




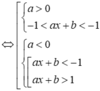
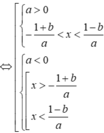
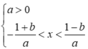
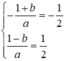


 Nhãnđ
Nhãnđ
