Với giá trị nào của m, đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = x 3 - 3 x 2 + 3 m x + 1 - m tạo với đường thẳng Δ: 3x + y - 8 = 0 một góc 45 ° ?
A. m = 0
B. m = 2
C. m = 3 4
D. m = 2 hoặc m = 3 4
Cho hàm số y= x3-3x2-mx+2 với m là tham số thực. Tìm giá trị của m để đường thẳng đi qua hai điểm cực trị của đồ thị hàm số tạo với đường thẳng d ; x+4y-5=0 một góc α = 45 ° .
A. m= -1/2
B. m= 1/2
C. m=0
D. m= 1
Ta có y’=3x2-6x-m
Để đồ thị hàm số đã cho có hai điểm cực trị khi phương trình y’=0 có hai nghiệm phân biệt ⇔ ∆ ' = 9 + 3 m > 0 ⇔ m > - 3
Ta có 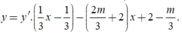
đường thẳng đi qua hai điểm cực trị Avà B là 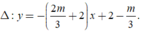
Đường thẳng d; x+4y-5=0 có một VTPT là n d → = ( 1 ; 4 ) .
Đường thẳng 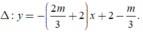 có một VTCP là
n
∆
→
=
(
2
m
3
+
2
;
1
)
có một VTCP là
n
∆
→
=
(
2
m
3
+
2
;
1
)
Ycbt suy ra:
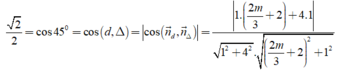
Suy ra
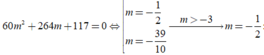 thỏa mãn
thỏa mãn
Chọn A.
Với cặp giá trị nào của a ; m thì đường thẳng ax + y + m = 0 đi qua hai điểm cực trị của đồ thị hàm số y = x 3 − 3 x 2 − 4 ?
A. 2 ; 4
B. 4 ; - 2
C. 4 ; 2
D. - 2 ; 4
Với cặp giá trị nào của (a;m) thì đường thẳng ax+y+m=0 đi qua hai điểm cực trị của đồ thị hàm số y = x 3 - 3 x 2 - 4 ?
A. (4:2)
B. (4; −2)
C. (−2;4)
D. (2;4)
Tìm tổng tất cả các giá trị thực của tham số m sao cho đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = 2 x 3 + 3 ( m - 1 ) x 2 + 6 m ( 1 - 2 m ) x song song đường thẳng y= -4x.
![]()
![]()
![]()
![]()
Tìm tổng tất cả các giá trị thực của tham số
m sao cho đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
\(y=2x^3+3\left(m-1\right)x^2+6m\left(1-2m\right)x.\) song song đường thẳng y= -4x
.
Chứng minh công thức tổng quát phương trình đi qua 2 điểm cực trị:
giả sử hàm bậc 3: \(y=ax^3+bxx^2+cx+d\left(a\ne0\right)\) có 2 điểm cực trị x1;x2
Ta đi tìm số dư 1 cách tổng quát:
Ta có: \(y'=3ax^2+2bx+c-và-y''=6ax+b\)
Xét phép chia giữa y' và y'' ta có: \(y=y'\left(\dfrac{1}{3}x+\dfrac{b}{9a}\right)+g\left(x\right)\left(1\right)\) là phường trình đi qua 2 điểm cực trị của đồ thị hàm số bậc 3
từ (1) Ta có: \(y=y'\dfrac{3ax+b}{9a}+g\left(x\right)-hay-y=y'\dfrac{6ax+2b}{18a}g\left(x\right)\)
Từ đây dễ suy ra: \(g\left(x\right)=y-\dfrac{y'.y''}{18a}\left(công-thức-tổng-quát\right)\) ( dĩ nhiên bạn chỉ cần nhớ cái này )
áp dụng vào bài toán ta có:
\(2x^3+3\left(m-1\right)x^2+6m\left(1-2m\right)x-\left(6x^2+6\left(m-1\right)x+6m\left(1-2m\right)\right).\dfrac{12x+6\left(m-1\right)}{18.2}\)
Gán: \(\left\{{}\begin{matrix}x=i\\m=10\end{matrix}\right.\) => 1710-841i
\(\Rightarrow y=4m\left(-2m-1\right)x+17m^2+m\) bài toán quay trở về bài toán đơn giản bạn giải nốt là oke
Cho hàm số y = 2 x 3 - 3 m 2 - m + 1 x 2 + 6 m 2 - 6 m x , với m là tham số. Gọi S là tập hợp các giá trị của m để đồ thị hàm số đã cho có hai điểm cực trị, đồng thời đường thẳng đi qua hai điểm cực trị đó vuông góc với đường thẳng y = x + 2 . Số phần tử của tập hợp S là
A. 2
B. 3
C. 1
D. 4
Chọn đáp án D
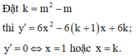
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi k ≠ 1
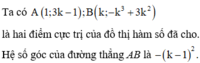
Đường thẳng AB vuông góc với đường thẳng y = x + 2 khi và chỉ khi

Cho hai hàm số y = (m - 1)x + 3 và y = (3 - m)x + 1, Với giá trị nào của m thì đồ thị của hai hàm só là hai đường thẳng song song với nhaub, Với giá trị nào của m thì đồ thị của 2 hàm số là hai đường thẳng cắt nhau
a: Để hai đường thẳng song song thì m-1=3-m
=>2m=4
hay m=2
\(\text{//}\Leftrightarrow m-1=3-m\Leftrightarrow m=2\\ \cap\Leftrightarrow m-1\ne3-m\Leftrightarrow m\ne2\)
Tìm tất cả các giá trị thực của tham số \(m\) để khoảng cách từ điểm \(M\left(0;3\right)\) đến đường thẳng đi qua hai điểm cực trị của đồ thị hàm số \(y=x^3+3mx+1\) bằng \(\dfrac{2}{\sqrt{5}}\)
Ta có : \(y'=3x^2+3m\)
Điều kiện để hàm số có 2 điểm cực trị là y'=0 có 2 nghiệm phân biệt
\(\Leftrightarrow 3x^2=-3m\) có 2 nghiệm phân biệt
\(\Leftrightarrow m<0\)
Đường thẳng đi qua 2 điểm cực trị là phần dư khi lấy y chia cho y':
\(x^3+3mx+1=\dfrac{x}{3}.(3x^2+3m)+2mx+1\)
\(=>\) đường thẳng đi qua 2 điểm cực trị có dạng: \(y=2mx+1\)
\(\Leftrightarrow 2mx-y+1=0\) \((\Delta)\)
\(d_{(M,\Delta)}=\dfrac{|0.2m+3.(-1)+1|}{\sqrt{4m^2+1}}=\dfrac{2}{\sqrt{5}}\)
\(\Leftrightarrow 4m^2+1=5 \Leftrightarrow m^2=1 \Leftrightarrow m=\pm1\)
Đối chiếu với điều kiện ta được \(m=1\)
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x 3 + 2 x 2 + m - 3 x + m có 2 điểm cực trị và điểm M(9;-5) nằm trên đường thẳng đi qua hai điểm cực trị của đồ thị hàm số.
A. m = 3
B. m = 2
C. m = -5
D. m = -1