Cho hàm số y = ( cos x - 1 ) / ( cos x + 2 ) . Mệnh đề nào trong số các mệnh đề sau đây là sai?
A. Tập xác định của hàm số là ℝ.
B. Hàm số có giá trị lớn nhất bằng 0.
C. Hàm số có giá trị nhỏ nhất bằng - 2.
D. Hàm số tuần hoàn với chu kì T = 2.
Cho các mệnh đề sau đây:
(1) Hàm số f ( x ) = log 2 2 x - log 2 x 4 + 4 có tập xác định D = [ 0 ; + ∞ )
(2) Hàm số y = log a x có tiệm cận ngang
(3) Hàm số y = log a x ; 0 < a < 1 và Hàm số y = log a x , a > 1 đều đơn điệu trên tập xác định của nó
(4) Bất phương trình: log 1 2 5 - 2 x 2 - 1 ≤ 0 có 1 nghiệm nguyên thỏa mãn.
(5) Đạo hàm của hàm số y = ln 1 - cos x là sin x 1 - cos x 2
Hỏi có bao nhiêu mệnh đề đúng:
A. 0
B. 2
C. 3
D.1
Cho hàm số f(x) = cos 2x và g(x) = tan 3x, chọn mệnh đề đúng
A. f(x) là hàm số chẵn, g(x) là hàm số lẻ
B. f(x)là hàm số lẻ, g(x) là hàm số chẵn.
C. f(x)là hàm số lẻ, g(x) là hàm số chẵn
D. f(x) và g(x) đều là hàm số lẻ.
Cho hàm số y = 2 x − 3 4 − x . Trong các mệnh đề sau, mệnh đề nào đúng ?
A. Đồ thị hàm số trên không có điểm cực trị
B. Giao hai tiệm cận là điểm I − 2 ; 4 .
C. Đồ thị hàm số trên có tiệm cận ngang x=4
D. Đồ thị hàm số trên có tiệm cận đứng y= -2
Đáp án A
Dễ có f’(x) < 0 với mọi giá trị của x trong TXĐ. Do đó hàm số đã cho không có cực trị.
Chọn phương án A.
Cho hàm số y = x + 1 1 - x và các mệnh đề sau
(1) Hàm số trên nhận điểm I(1;-1) làm tâm đối xứng,
(2) Hàm số trên nhận đường thẳng y = -x làm trục đối xứng.
(3) Hàm số trên nhận y = -1 là tiệm cận đứng.
(4) Hàm số trên luôn đồng biến trên R.
Trong số các mệnh đề trên, số mệnh đề sai là
A. 1
B. 2
C. 3
D. 4
Chọn B
+ Hàm số có tiệm cận đứng x=1 và tiệm cận ngang y= -1. Giao điểm của hai đường tiệm cận là I(1; -1) là tâm đối xứng của đồ thị. Mệnh đề 1 đúng, mệnh đề 3 sai.
+ Vì đường thẳng y=-x là một phân giác của góc tạo bởi 2 đường tiệm cận nên đường thẳng y=-x là một trục đối xứng của đồ thị hàm số. Mệnh đề 2 đúng.
+ Hàm số có tập xác định là R\{1}, nên hàm số không thể luôn đồng biến trên R.Mệnh đề 4 sai.
Cho hàm số y = x + x 2 - x + 1 . Mệnh đề trong các mệnh đề sau là đúng?
A. Đồ thị hàm số đã cho chỉ có 1 tiệm cận ngang
B. Đồ thị hàm số đã cho chỉ có 1 tiệm cận đứng.
C. Đồ thị hàm số đã cho có 2 tiệm cận đứng.
D. Đồ thị hàm số đã cho có 1 tiệm cận đứng và 1 tiệm cận ngang
Tập xác định: D = R
Ta có:
lim x → - ∞ = lim x → - ∞ x + x 2 - x + 1 = lim x → - ∞ x - 1 x - x 2 - x + 1 = 2 2
Do đó đồ thị của hàm số có một tiệm cận ngang là y = 2 2
Đáp án A
Cho hàm số f x = 3 x + 1 − x + 1 . Trong các mệnh đề sau mệnh đề nào đúng?
A. f x nghịch biến trên R
B. f x đồng biến trên − ∞ ; 1 v à 1 ; + ∞
C. f x nghịch biến trên − ∞ ; 1 ∪ 1 ; + ∞
D. f x đồng biến trên R
Đáp án B
Ta có: f ' x = 4 − x + 1 2 > 0 ∀ x ≠ 1
Do đó f(x) đồng biến trên − ∞ ; 1 và 1 ; + ∞ .
Gọi (C) là đồ thị hàm số y = x + 2 2 x - 1 . Trong các mệnh đề sau, mệnh đề nào sai?
A. (C) có tiệm cận ngang là y = 1 2
B. (C) có đúng một trục đối xứng.
C. (C) có tiệm cận đứng là x = 1 2
D. (C) có đúng một tâm đối xứng.
2) Cho △ABC thỏa mãn hệ thức \(b+c=2a\). Mệnh đề nào trong các mệnh đề sau đúng?
\(A.\cos B+\cos C=2\cos A\)
\(B.\sin B+\sin C=2\sin A\)
\(C.\sin B+C=\dfrac{1}{2}\sin A\)
\(D.\sin B+\cos C=2\sin A\)
Cho a, b, c là ba số dương khác 1. Đồ thị các hàm số y = log a x , y = log b x , y = log c x được cho trong hình vẽ bên. Mệnh đề nào dưới đây là mệnh đề đúng?

A. a < b < c
B. c < a < b
C. c < b < a
D. b < c < a
Cho hàm số y = f(x) liên tục trên R , có đồ thị của đạo hàm f'(x) như sau:
Trong các mệnh đề sau, mệnh đề nào sai?
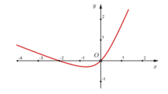
A. f đạt cực tiểu tại x = 0
B. f đạt cực tiểu tại x =-2
C. f đạt cực đại tại x = -2
D. Cực tiểu của f nhỏ hơn cực đại
Đáp án B
Nhìn đồ thị, ta thấy f' đổi dấu từ dương sang âm khi đi qua điểm x = -2, do đó x = -2 là điểm cực đại của hàm f => C đúng, B sai.
Tương tự, f’ đổi dấu từ âm sang dương khi đi qua điểm x = 0, do đó x = 0 là điểm cực tiểu của hàm f => A đúng.
