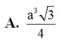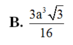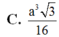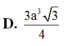Cho lăng trụ ABCA′B′C′, đáy là tam giác đều cạnh bằng a, tứ giác ABB′A′ là hình thoi, A ' AC ^ = 60 o , B ' C = a 3 2 . Tính thể tích lăng trụ ABCA′B′C′.
A. 3 a 3 4
B. 3 3 a 3 4
C. 3 3 a 3 16
D. 3 a 3 16
Cho lăng trụ ABCA’B’C’, đáy là tam giác đều là cạnh bằng a, tứ giác ABB’A’ là hình thoi, Tính thể tích lăng trụ ABCA’B’C’.
A. 3 3 a 3 16
B. 3 3 a 3 4
C. 3 a 3 4
D. 3 a 3 16
Đáp án A
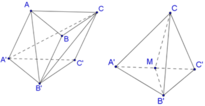
Dễ dàng tính được các cạnh của tứ diện CA’B’C’:


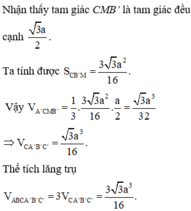
Cho lăng trụ ABCA’B’C’, đáy là tam giác đều là cạnh bằng a, tứ giác ABB’A’ là hình thoi, A ' A C ^ = 60 o , B ' C ' = a 3 2 Tính thể tích lăng trụ ABCA’B’C’.
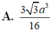
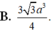
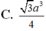
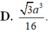
Chọn A
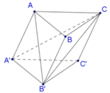
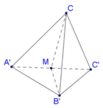
Dễ dàng tính được các cạnh của tứ diện CA’B’C’:

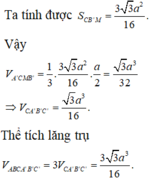
Cho hình lăng trụ tứ giác đều, cạnh đáy bằng a, cạnh bên bằng b. Diện tích toàn phần của hình lăng trụ là
A. S t p = 2 a 2 + 4 a b .
B. S t p = 2 a 2 + 16 a b .
C. S t p = a 2 + 4 a b .
D. S t p = a 2 + 16 a b .
Đáp án A
S t p = S x q + 2 S d , trong đó S t p là diện tích toàn phần, S d là diện tích đáy, S x q là diện tích xung quanh hình lăng trụ tứ giác đều.
S t p = 4. a . b + 2 a 2 = 2 a 2 + 4 a b .
Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a, hình chiếu vuông góc của A' lên đáy (ABC) trùng với trọng tâm của tam giác ABC và cạnh bên tạo với đáy một góc bằng 60 ° . Thể tích của hình lăng trụ là:
A. 3 a 3 12 B. 3 a 3 8
C. 3 a 3 4 D. 3 a 3 2
Chọn C.
Gọi H là trọng tâm của tam giác ABC. Khi đó chiều cao của lăng trụ bằng A'H = AH.tan60 °
Tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng có chiều cao h và đáy lần lượt là:
a) Hình vuông cạnh a;
b) Tam giác đều cạnh a;
c) Lục giác đều cạnh a;
d) Hình thang cân, đáy lớn là 2a, các cạnh còn lại bằng a;
e) Hình thoi có hai đường chéo là 6a và 8a.
Gọi h là chiều cao của hình lăng trụ đứng.

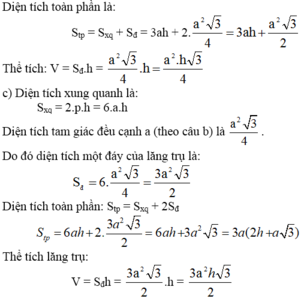


Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a, đỉnh A’ cách đều ba đỉnh A, B, C. Cạnh bên AA’ tạo với đáy một góc 45 ° Thể tích khối lăng trụ ABC.A’B’C’ bằng bao nhiêu?
A. a 3 10 10
B. a 3 3 12
C. a 3 4
D. a 3 8
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a, đỉnh A’ cách đều ba đỉnh A, B, C. Cạnh bên AA’ tạo với đáy một góc 45 0 . Thể tích khối lăng trụ ABC.A’B’C’ bằng bao nhiêu?
A . a 3 3 10
B . a 3 3 12
C . a 3 4
D . a 3 8
Đáp án là C
Gọi G là trọng tâm của tam giác ABC.
Do tam giác ABC đều cạnh a nên 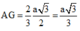
Diện tích tam giác ABC bằng a 3 3 4
Do đỉnh A’ cách đều ba đỉnh A, B, C nên A'G ⊥ (ABC) => A'G là đường cao của khối lăng trụ.
Theo giả thiết, ta có
A
'
A
G
^
=
45
0
=>
∆
A'GA vuông cân. Tù đó suy ra ![]()
Vậy thể tích của khối lăng trụ bằng ![]()
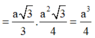
Cho lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a, mặt bên ABB'A' là hình thoi A ' A C ^ = 60 ∘ ; B ' C = a 3 2 . Tính thể tích khối lăng trụ ABC.A'B'C'.
A. a 3 3 4
B. 3 a 3 3 16
C. a 3 3 16
D. 3 a 3 3 4
Cho lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a, mặt bên ABB'A' là hình thoi A A ' C ⏜ = 60 0 ; B'C= a 3 2 .Tính thể tích khối lăng trụ ABC.A'B'C'.