Phát biểu định nghĩa tiếp tuyến của đường tròn. Phát biểu tính chất của tiếp tuyến và dấu hiệu nhận biết tiếp tuyến. Phát biểu các tính chất của hai tiếp tuyến cắt nhau.

Những câu hỏi liên quan
Phát biểu định nghĩa tiếp tuyến của đường tròn. Phát biểu tính chất của tiếp tuyến và dấu hiệu nhận biết tiếp tuyến. Phát biểu các tính chất của hai tiếp tuyến ?
- Tiếp tuyến với đường tròn là đường thẳng chỉ có một điểm chung với đường tròn.
-Tiếp tuyến với đường tròn thì vuông góc với bán kính đi qua tiếp điểm.
- Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua tiếp điểm ấy thì đường thẳng ấy là một tiếp tuyến của đường tròn.
- Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì:
a)Điểm đó cách đều hai tiếp điểm.
b)Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
c)Tia kẻ từ tâm qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm
Đúng 0
Bình luận (0)
( Tiếp theo )5. Phát biểu dấu hiệu ( định lí ) nhận biết hai đường thẳng song song.6. Phát biểu tiên đề Ơ-clit về đường thẳng song song.7. Phát biểu định lí về hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba.8. Phát biểu tính chất ( định lí ) của hai đường thẳng song song.
Đọc tiếp
( Tiếp theo )
5. Phát biểu dấu hiệu ( định lí ) nhận biết hai đường thẳng song song.
6. Phát biểu tiên đề Ơ-clit về đường thẳng song song.
7. Phát biểu định lí về hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba.
8. Phát biểu tính chất ( định lí ) của hai đường thẳng song song.
5. Dấu hiệu ( định lí ) nhận biết 2 đường thẳng song song:
+ Nếu đường thẳng c cắt hai đường thẳng a,b và trong các góc tạo thành có 1 cặp góc so le trong bằng nhau ( hoặc góc đồng vị bằng nhau ) thì a và b song song với nhau
6. Tiên đề Ơ - clit về đường thẳng song song:
Qua 1 điểm nằm ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó
7, Định lí về hài đường thẳng phân biệt cùng vuông góc với đường thẳng thứ 3
Nếu 2 đường thẳng phân biệt cùng vuông góc với đường thẳng thứ 3 thì chúng song song với nhau
8. Tính chất ( định lí ) của 2 đường thẳng song song:
Nếu 1 đường thẳng cắt 2 đường thẳng song song thì
1. Hai góc đồng vị bằng nhau
2. Hai góc so le trong bằng nhau
3. Hai góc trong cùng phía bù nhau
Đúng 0
Bình luận (0)
5. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le trong bằng nhau thì hai đường thẳng song song.
\(\widehat{A_1}=\widehat{B}_1\Rightarrow a//b\)
- Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc đồng vị bằng nhau thì hai đường thẳng song song.
\(\widehat{A}_3=\widehat{B}_1\Rightarrow a//b\)
- Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc trong cùng phía bù nhau thì hai đường thẳng song song.
\(\widehat{A}_2+\widehat{B}_1=180^0\Rightarrow a//b\)
Đúng 0
Bình luận (0)
6.Qua một điểm nằm ngoài đường thẳng,chỉ có một đường thẳng song song với đường thẳng đó
7. Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song với nhau \(\hept{\begin{cases}a\perp b\\b\perp c\end{cases}\Rightarrow}a//b\)
8.Nếu một đường thẳng cắt hai đường thẳng // thì :
a, 2 góc so le trong bằng nhau
b, 2 góc đồng vị bằng nhau
c, 2 góc trong cùng phía bù nhau
Đúng 0
Bình luận (0)
Phát biểu định nghĩa tính chất 3 đường trung tuyến của tam giác vẽ hình và ghi giả thuyết kết luận
Tính chất ba đường trung tuyến của tam giác
Định lý: Ba đương trung tuyến của tam giác cùng đi qua điểm. điểm đó cách đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.
Giao điểm của ba đường trung tuyến gọi là trọng tâm
GT : G là trọng tâm ∆ ABC
KL : AG/AD = BG/BE = CG/CF = 2/3
Đúng 2
Bình luận (2)
TK:https://loigiaihay.com/ly-thuyet-tinh-chat-ba-duong-trung-tuyen-cua-tam-giac-c42a5574.html
Đúng 0
Bình luận (0)
từ 1 điểm M cố định ở bên ngoài đường tròn (O), kẻ 1 tiếp tuyến MT(T là tiếp điểm) và 1 cát tuyến MAB của đường tròn đó
a)C/m: MT2=MA.MB
b) trường hợp cát tuyến MAB đi qua tâm O. cho MT=20cm và cát tuyến dài nhất cùng xuất phát từM=50cm. tính bán kính R của đường tròn tâm O
a: Xét ΔMTA và ΔMBT có
\(\widehat{MTA}=\widehat{MBT}\left(=\dfrac{1}{2}sđ\stackrel\frown{AT}\right)\)
\(\widehat{TMA}\) chung
Do đó: ΔMTA đồng dạng với ΔMBT
=>\(\dfrac{MT}{MB}=\dfrac{MA}{MT}\)
=>\(MT^2=MA\cdot MB\)
b: \(MT^2=MA\cdot MB\)
=>\(MA\cdot MB=20^2=400\)
=>\(MA=\dfrac{MT^2}{MB}=\dfrac{400}{50}=8\left(cm\right)\)
MA+AB=MB
=>AB+8=50
=>AB=42(cm)
=>R=42/2=21(cm)
Đúng 1
Bình luận (0)
Phát biểu định nghĩa, tính chất của hai góc đối đỉnh.
Câu 2: Nêu định nghĩa về: hai đường thẳng vuông góc, đường trung trực của một đoạn thẳng.
Câu 3: Nêu dấu hiệu nhận biết hai đường thẳng song song. Nêu tính chất của hai đường thẳng song song. Phát biểu tiên đề Ơclit
Câu 1:
Hai góc đối đỉnh là hai góc có chung đỉnh, và hai tia của góc này là hai tia đối của hai tia của góc kia
Tính chất: Hai góc đối đỉnh thì bằng nhau
Đúng 1
Bình luận (0)
Câu 1 :- định nghĩa : 2 góc đối đỉnh là 2 góc mà là mỗi cạnh của góc này là tia đối của một cạnh của góc kia
- tính chất : 2 góc đối đỉnh thì bằng nha
Đúng 0
Bình luận (0)
Câu 2. Hai đường thẳng vuông góc: Khi a cắt b tạo thành 1 góc 90 độ .
đường trung trực của đoạn thẳng: Khi a vuông góc với b tại trung điểm của đt b.
Đúng 0
Bình luận (0)
Cho hai đường tròn (O,R)và (O`,r) tiếp xúc ngoài tại A kẻ tiếp tuyến chung ngoài DE của (O)và (O`), D€(O),E€(O')tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài DE ở I
a,tính số đo góc OIO'.
b, chứng minh OO' là tiếp tuyến của đường tròn đường kính DE
c, tính độ dài DE theo R và r
a: Xét (O) có
ID,IA là các tiếp tuyến
Do đó: IO là phân giác của góc DIA
=>\(\widehat{DIA}=2\cdot\widehat{OIA}\)
Xét (O') có
IA,IE là các tiếp tuyến
Do đó: IO' là phân giác của góc AIE
=>\(\widehat{AIE}=2\cdot\widehat{AIO'}\)
Ta có: \(\widehat{DIA}+\widehat{EIA}=180^0\)(hai góc kề bù)
=>\(2\left(\widehat{OIA}+\widehat{O'IA}\right)=180^0\)
=>\(2\cdot\widehat{OIO'}=180^0\)
=>\(\widehat{OIO'}=90^0\)
b: Xét (O) có
ID,IA là các tiếp tuyến
Do đó: ID=IA
Xét (O') có
IA,IE là các tiếp tuyến
Do đó: IA=IE
Ta có: IA=IE
ID=IA
Do đó: ID=IE
=>I là trung điểm của DE
=>I là tâm đường tròn đường kính DE
Xét ΔDAE có
AI là bán kính
\(AI=\dfrac{DE}{2}\)
Do đó: ΔADE vuông tại A
=>A nằm trên (I)
Xét (I) có
IA là bán kính
O'O\(\perp\)IA tại A
Do đó: OO' là tiếp tuyến của (I)
=>O'O là tiếp tuyến của đường tròn đường kính DE
Đúng 3
Bình luận (0)
4. Từ M cố định bên ngoài đường tròn (o) kẻ môt tiếp tuyến MT ( T là tiếp điểm ) và một cát tuyến MAB của đường tròn đó
a) Chứng minh MT2 = MA.MB
b) trường hợp cát tuyến MAB đi qua tâm (o) . Cho MT = 20 (cm) và cát tuyến dài nhất cũng xuất phát từ M = 50 (cm) . Tính R của (O)
Giúp em bài này với mai em cần gấp !
a: Xét ΔMTA và ΔMBT có
\(\widehat{MTA}=\widehat{MBT}\)
\(\widehat{TMA}\) chung
DO đó: ΔMTA∼ΔMBT
Suy ra: MT/MB=MA/MT
hay \(MT^2=MA\cdot MB\)
b: MB=50cm
=>MA=8cm
=>AB=42cm
=>R=21cm
Đúng 1
Bình luận (0)
1) Cho (I;2cm) (O) đường kính 8cm tiếp xúp tại C, AB là tiếp tuyến của hai đường tròn. Tính tứ giác ABOI
2) Cho (O;3cm)(I;1cm) tiếp xúp tại C tiếp tuyến chung AB của hai đường tròn cắt OI tại M. Tính MC
3) Cho (O;12cm)(O'16cm) chát nhau tại A và B sao cho OA là tiếp tuyến của đường tròn (O'). Tính dây AB
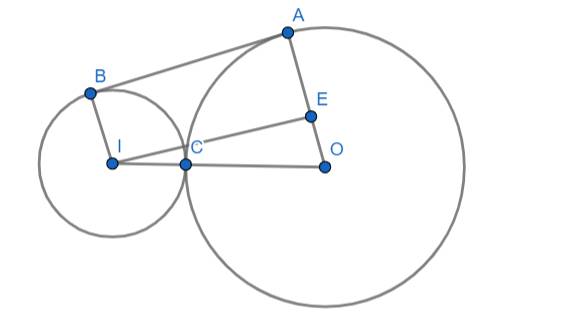
Do AB là tiếp tuyến chung của (O) và (I) nên:
\(\left\{{}\begin{matrix}\widehat{IBA}=90^o\\\widehat{OAB}=90^o\end{matrix}\right.\) (tiếp tuyến vuông góc với bán kính)
\(\Rightarrow\left\{{}\begin{matrix}IB\perp AB\\OA\perp AB\end{matrix}\right.\)
\(\Rightarrow IB//OA\) (cùng vuông góc với AB)
\(\Rightarrow ABOI\) là hình thang
Ta kẻ IE vuông góc với OA tại E
⇒ IEAB là hình chữ nhật
⇒ \(IB=AE=2\left(cm\right)\) (cặp cạnh đối của hình chữ nhật)
\(\Rightarrow OE=OA-AE=8-2=6\left(cm\right)\)
Mà: \(OI=OC+IC=2+8=10\left(cm\right)\)
Xét ΔIEO vuông tại E áp dụng định lý Py-ta-go ta có:
\(IO^2=OE^2+IE^2\)
\(\Leftrightarrow10^2=6^2+IE^2\)
\(\Leftrightarrow IE=\sqrt{100-36}=\sqrt{64}\)
\(\Leftrightarrow IE=8\left(cm\right)\)
Mà: \(AB=IE=8\left(cm\right)\) (ABIE là hình chữ nhật)
Diện tích của tứ giác ABOI có AB là đường cao là:
\(S_{ABOI}=\dfrac{\left(IB+OA\right)\cdot AB}{2}=\dfrac{\left(2+8\right)\cdot8}{2}=40\left(cm^2\right)\)
Đúng 3
Bình luận (0)
Phát biểu định lí về góc tạo bởi tia tiếp tuyến và dây cung.
Định lí thuận: Góc tạo bởi tia tiếp tuyến và dây cung có số đo bằng nửa số đo của cung bị chắn.
Định lí đảo: Một góc có đỉnh nằm trên đường tròn, một cạnh chứa dây cung, có số đo bằng nửa số đo cung căng dây đó và cung này nằm bên trong góc thì cạnh kia là một tia tiếp tuyến.
Đúng 0
Bình luận (0)






















