Cho hàm số y = x 3 + 17 x 2 - 24 x + 8 . Kết luận nào sau đây là đúng?
A. x C D = 1
B. x C D = 2 3
C. x C D = - 3
D. x C D = - 12
cho hàm số y = f(x) = \(x^2\)-8
a, tính f(3);f(-2)
b, tìm x khi biết giá trị tương ứng y là 17
a.
\(f\left(3\right)=3^2-8=9-8=1\)
\(f\left(-2\right)=\left(-2\right)^2-8=4-8=-4\)
b.
\(y=17\Rightarrow x^2-8=17\)
\(\Rightarrow x^2=25\)
\(\Rightarrow x=\pm5\)
Cho hàm số y = (12 - m)x + 2m - 3. Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng -17 khi m =
Giao điểm của đồ thị hàm số với trục tung là điểm có hoành độ bằng 0.
Thay x = 0 ta có : y = 2m - 3.
Để y = -17 thì \(2m-3=-17\Leftrightarrow2m=-14\Leftrightarrow m=-7.\)
Giao điểm của đồ thị hàm số với trục tung là điểm có hoành độ bằng 0.
Thay x = 0 ta có : y = 2m - 3
Để y = -17 thì \(2m-3=-17\Leftrightarrow2m=-14\Leftrightarrow m=-7.\)
Giao điểm của đồ thị hàm số với trục tung là điểm có hoành độ bằng 0
Thay x=0 ta có: y=m-3
Để y=-17 thì 2m-3=-17<=>2m=-14<=>m=-7
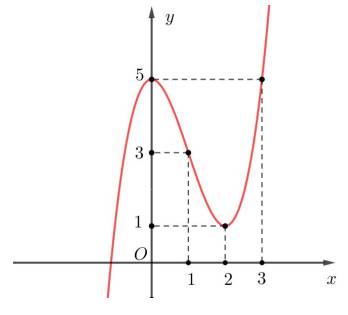
Cho hàm số y=f(x) có đồ thị như hình vẽ. Hỏi phương trình \(f\left(x^3-2x^2+14x+\sqrt{17}\right)=\sqrt{17}\) có bao nhiêu nghiệm thực?
Cho hàm số: y=f(x)=x2-8
Tìm x biết y=17
\(y=f\left(x\right)=x^2-8\)
Thay \(y=17\) ta có:
\(17=x^2-8\)
\(\Rightarrow x^2=25\)
\(\Rightarrow x=5\) hoặc \(x=-5\)
Vậy \(x\in\left\{5;-5\right\}\)
Có hàm số y = f(x) = x2 - 8. Với y = 17
=> x2 - 8 = 17
x2 = 17 + 8
x2 = 25
=> x2 = 52
=> x = 5
Vậy với đồ thị hàm số y = f(x) = x2 - 8 và y = 17 thì ta có x = 5
Có hàm số y = f(x) = x2 - 8. Với y = 17
=> x2 - 8 = 17
=> x2 = 17 + 8
x2 = 25
=> x2 = 52 hoặc x2 = ( -5 )2
Vậy với đồ thị hàm số y = f(x) = x2 - 8 và y = 17 thì ta tìm được x = -5 hoặc x = 5
cho hàm số Y=F(x)=x mũ 2 + 2 nhân x - 3 khẳng định nào sau đây là đúng
a.F(1)=1 b.F(1 phần 2 ) = -7 phần 4 c.F(-1 phần 2 ) = -17 phần 4 d.F(3)=9
cho hàm số Y=F(x)=1 phần 2 nhân x mũ 2 - 5 khẳng đình nao sau đây là đúng
a.F(1)=-9 phần 2 b.F(2)= -5 c.F(-1 phần 2 ) = 39 phần 8 d.F(0)=5
giúp mik nhé mn :))
Cho hàm số y = f(x) = x^2 - 8
tìm x biết y + 17
giúp mik với
a) Cho hàm số y=f(x)=ax5+bx3+cx-5 (a,b,c thuộc R)
Cho f(-3)=208. Tính f(3)=?
b) Cho hàm số y=g(x)=ax4-bx2+x+3 (a,b thuộc R)
Cho g(2)=17. Tính g(-2)=?
1/Tìm x,y,z khi x/6=y/4=z/3 và x+y-z=-21
2/cho hàm số :y=f(x)=x^2-8
a) tính f(3);f(-2)
b)tìm x biết giá trị của y=17
1/ \(\frac{x}{6}=\frac{y}{4}=\frac{z}{3}vàx+y-z=-21\)
-Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{6}=\frac{y}{4}=\frac{z}{3}=\frac{x+y-z}{6+4-3}=\frac{-21}{7}=-3\)
-Suy ra: \(\frac{x}{6}=-3\Rightarrow x=-18\)
\(\frac{y}{4}=-3\Rightarrow y=-12\)
\(\frac{z}{3}=-3\Rightarrow z=-9\)
vậy x=-18;y=-12;z=-9
2) a/y=f(x)=x^2-8
\(\Rightarrow\)y= f(3)=3^2-8=1
\(\Rightarrow\)y=f(-2)=(-2)^2-8=-4
vậy f(3)=1;f(-2)=-4
b/y=17=x^2-8
x^2-8=17
x^2=17+8
x^2=25
x^2=5^2
x=5
vậy x=5
Cho hàm số y=f(x) có đạo hàm f'(x) liên tục trên [1;4], f(1)=12 và ∫ 1 4 f ' ( x ) d x = 17 Giá trị của f(4) bằng
![]()
![]()
![]()
![]()
Cho hàm số y=f(x) có đạo hàm f'(x) liên tục trên đoạn [1;4], f(1)=12 và ∫ 1 4 f ' ( x ) d x = 17 . Giá trị của f(4) bằng:
A. 29
B. 5
C. 19
D. 9