Cho hình chóp S. ABC có các góc tại đỉnh S cùng bằng 60 0 , SA = a, SB = 2a, SC = 3a . Tính khoảng cách từ đỉnh A đến mặt phẳng (SBC).
![]()
![]()
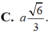
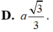
Cho hình chóp S.ABC có các góc tại đỉnh S cùng bằng 60 ° , S A = a , S B = 2 a , S C = 3 a . Tính khoảng cách từ đỉnh A đến mặt phẳng (SBC)
A. a 3
B. a 6
C. a 6 3
D. a 3 3
Chọn C.
Phương pháp: Sử dụng công thức tính thể tích khối chóp khi biết ba góc ở một đỉnh và ba cạnh ở đỉnh đó.
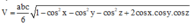
(trong đó a, b, c là độ dài ba cạnh, x, y, z là số đo ba góc ở một đỉnh)
Sau đó tính khoảng cách dựa vào công thức tính thể tích h = 3 V h .
Cách giải: Áp dụng công thức trên ta có:
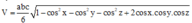
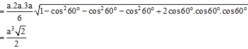

Cho hình chóp S.ABC có các góc tại đỉnh S cùng bằng 600, SA = a, SB = 2a, SC = 3a. Tính khoảng cách từ đỉnh A đến mặt phẳng (SBC)
![]()
![]()
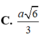
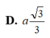
Cho hình chóp S.ABC có SA, SB, SC tạo với mặt đáy các góc bằng nhau và bằng 60 ⁰ . Biết BC=a, B A C ^ = 45 ° . Tính khoảng cách h từ đỉnh S đến mặt phẳng (ABC)
A. h = a 6
B. h = a 6 2
C. h = a 6 3
D. h = a 6
Cho hình chóp S.ABC có SA, SB, SC tạo với mặt đáy các góc bằng nhau và bằng 60 ⁰ . Biết B C = a , B A C ^ = 45 ° . Tính khoảng cách h từ đỉnh S đến mặt phẳng (ABC).
A. h = a 6 3
B. h = a 6
C. h = a 6
D. h = a 6 2
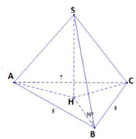
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại đỉnh B với AC = 2a, BC = a. Đỉnh S cách đều các điểm A, B, C. Biết góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 60 ° . Khoảng cách từ trung điểm M của SC đến mặt phẳng (SAB) bằng
A. a 39 13
B. 3 a 13 13
C. a 39 26
D. a 13 26
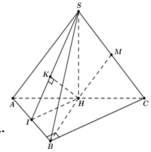
Gọi H là trung điểm của AC
Đỉnh S cách đều các điểm A, B, C ![]()
Xác đinh được ![]()
Ta có MH//SA ![]()
Gọi I là trung điểm của AB ![]()
![]() và chứng minh được
và chứng minh được ![]()
Trong tam giác vuông SHI tính được ![]()
Chọn A.
Cho hình chóp S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau và SA = a, SB = 2a, SC = 3a. Khoảng cách từ điểm S đến mặt phẳng (ABC) là
A. 5 a 6
B. 6 a 7
C. 7 a 6
D. 6 a 5
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại đỉnh B với AC =2a, BC =a. Đỉnh S cách đều các điểm A, B, C. Biết góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 60 o Khoảng cách từ trung điểm M của SC đến mặt phẳng (SAB) bằng
A. a 39 13
B. 3 a 13 13
C. a 39 26
D. a 13 26
Chọn A

Gọi H là trung điểm của AC. Đỉnh S cách đều các điểm A, B, C
=> SH ⊥ (ABC)
Xác đinh được
![]()
Ta có MH // SA
![]()
Gọi I là trung điểm của AB => HI ⊥ AB
![]()
và chứng minh được HK ⊥ (SAB)
![]()
Trong tam giác vuông SHI tính được
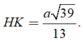
Cho hình chóp .S ABC có các cạnh bên SA, SB, SC tạo với đáy các góc bằng nhau và đều bằng 30 0 Biết AB = 5; AC = 8; BC = 7, khoảng cách từ A đến mặt phẳng (SBC) bằng
A. d = 35 139 13
B. d = 35 39 52
C. d = 35 13 52
D. d = 35 13 26
Cho hình chóp S.ABC có tam giác ABC là tam giác vuông cân tại S, SB = 2a và khoảng cách từ A đến mặt phẳng (SBC) bằng 3a. Tính theo a thể tích V của khối chóp S.ABC
A. V = 2 a 3
B. V = 4 a 3
C. V = 6 a 3
D. V = 12 a 3
Ta chọn (SBC) làm mặt đáy => chiều cao khối chóp là d(A, (SBC)) = 3a
Tam giác SBC vuông cân tại S nên ![]()
Vậy thể tích khối chóp ![]()
Chọn A.