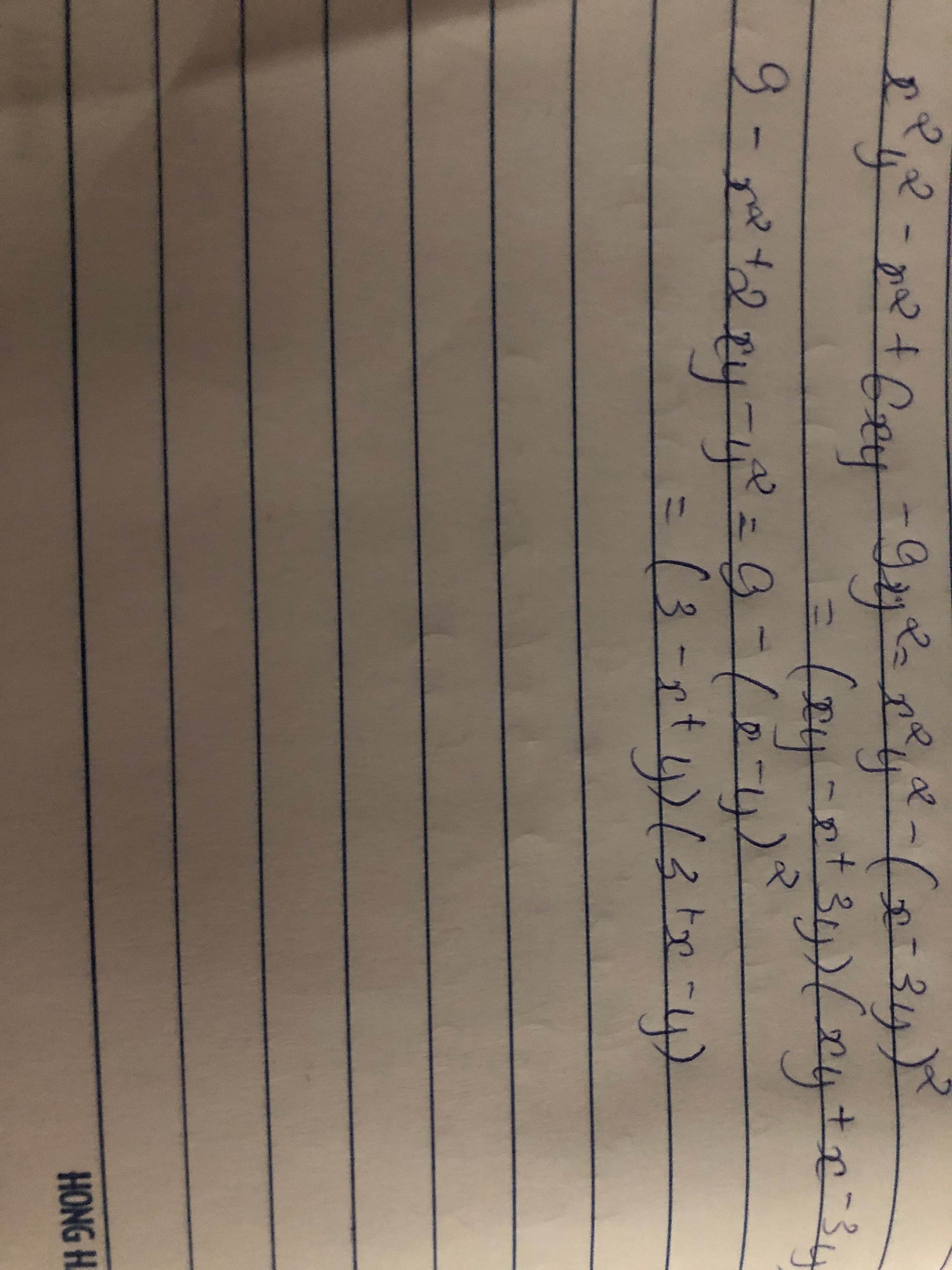Phân tích đa thức thành nhân tử: x^2-6xy+9y^2-36z

Những câu hỏi liên quan
Phân tích đa thức thành nhân tử : x^2 - 49 - 6xy + 9y^2
=[x2-6xy+(3y)2-49]
=[(x-3y)2-72]
=(x-3y-7)*(x+3y+7)
Đúng 0
Bình luận (0)
= x^2 - 6xy + 9y^2 - 49
= x^2 - 6xy + ( 3y )^2 - 49
= (x - 3y)^2 - 7^2
= (x - 3y -7)( x-3y +7) tk cho mk nha
Đúng 0
Bình luận (0)
\(x^2-49-6xy+9y^2\)
\(=\left(x^2-6xy+9y^2\right)-7^2\)
\(=\left(x-3y\right)^2-7^2\)
\(=\left(x-3y-7\right)\left(x-3y+7\right)\)
k mk nha ^_^
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử
a, \(x^2-y^2\)
b,\(x^2-6xy+9y^2-36\)
a. \(x^2-y^2=\left(x-y\right)\left(x+y\right)\)
b. \(x^2-6xy+9y^2-36=\left(x-3y\right)^2-6^2=\left(x-3y-6\right)\left(x-3y+6\right)\)
Đúng 2
Bình luận (0)
a: \(x^2-y^2=\left(x-y\right)\left(x+y\right)\)
b: \(x^2-6xy+9y^2-36=\left(x-3y\right)^2-6^2=\left(x-3y-6\right)\left(x-3y+6\right)\)
Đúng 2
Bình luận (0)
Phân tích đa thức thành nhân tử
x^2y^2-x^2+6xy-9y^2
9-x^2+2xy-y^2
a) Ta có: \(x^2y^2-x^2+6xy-9y^2\)
\(=x^2y^2-\left(x^2-6xy+y^2\right)\)
\(=\left(xy\right)^2-\left(x-3y\right)^2\)
\(=\left(xy-x+3y\right)\left(xy+x-3y\right)\)
b) Ta có: \(9-x^2+2xy-y^2\)
\(=9-\left(x^2-2xy+y^2\right)\)
\(=9-\left(x-y\right)^2\)
\(=\left(9-x+y\right)\left(9+x-y\right)\)
Đúng 0
Bình luận (0)
1,Phân tích đa thức thành nhân tử:
a,x2+6xy+9y2-3x-9y+2
x^2+6xy+9y^2-3x-9y+2
=( x^2+6xy+9y^2)-3(x+3y)+9/4 -1/4
=(x+3y)^2-3(x+3y)+(3/2)^2- 1/4
=(x+3y+3/2)^2-(1/2)^2
=(x+3y+3/2+1/2)(x+3y+3/2-1/2)=(x+3y+2)(x+3y+1)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử 3x^2-6xy+9y^2-12
\(3x^2-6xy+9y^2-12\)
\(=3\cdot x^2-3\cdot2xy+3\cdot3y^2-3\cdot4\)
\(=3\cdot\left(x^2-2xy+3y^2-4\right)\)
Đúng 1
Bình luận (0)
=3*x^2-3*2xy+3*3y^2-3*4
=3(x^2-2xy+3y^2-4)
Đúng 0
Bình luận (1)
Phân tích đa thức thành nhân tử
a) 2x^3 + 6xy - x^2*z - 3yz
b) x^2 - 6xy + 9y^2 - 49
a) \(2x^3+6xy-x^2z-3yz\)
= \(\left(2x^3+6xy\right)-\left(x^2z+3yz\right)\)
=\(2x\left(x^2+3y\right)-z\left(x^2+3y\right)\)
=\(\left(x^2+2y\right)\left(2x-z\right)\)
b)\(x^2-6xy+9y^2-49\)
=\(x^2-2.x.3y+\left(3y\right)^2-7^2\)
=\(\left(x-3y\right)^2-7^2\)
=\(\left(x-3y+7\right)\left(x-3y-7\right)\)
Đúng 0
Bình luận (0)
Phân tích đa thức sau thành nhân tử:
x2+9y2+6xy
=x^2 + 2 * x * 3y + (3y)^2
=(x + 3y)^2
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử:
a) 9y^2 + 9y - 6xy + x^2 - 3x -4
b) x^4 + 6x^3 + 13x^2 + 12x + 4
\(x^4+6x^3+13x^2+12x+4\)
\(=x^4+x^3+5x^3+5x^2+8x^2+8x+4x+4\)
\(=x^3\left(x+1\right)+5x^2\left(x+1\right)+8x\left(x+1\right)+4\left(x+1\right)\)
\(=\left(x+1\right)\left(x^3+5x^2+8x+4\right)\)
\(=\left(x+1\right)\left(x^3+x^2+4x^2+4x+4x+4\right)\)
\(=\left(x+1\right)\left[x^2\left(x+1\right)+4x\left(x+1\right)+4\left(x+1\right)\right]\)
\(=\left(x+1\right)^2\left(x+2\right)^2\)
Đúng 0
Bình luận (0)
Phân tích đa thức sau thành nhân tử: a) x^2-4x+4-y^2 b) x^2+6x-4y^2+9 c) x^2-6xy+9y^2-36
a) = (x - 2)2 - y2
= (x - 2 - y)(x + 2 + y)
b) = (x^2 + 6x + 9) - (2y)^2
= (x + 3)2 - (2y)2
= (x - 2y + 3)(x + 2y + 3)
c) = (x - 3y)2 - 62
= (x - 3y - 6)(x - 3y + 6)
Đúng 1
Bình luận (0)