Cho hình lăng trụ đều ABC.A'B'C' có tất cả các cạnh bằng a. Gọi M là trung điểm của AB và α là góc tạo bởi đường thẳng MC’ và mặt phẳng (ABC). Khi đó tan α bằng
A. 2 7 7
B. 3 2
C. 3 7
D. 2 3 3
Cho hình lăng trụ đều ABC.A'B'C' có tất cả các cạnh bằng a. Gọi M là trung điểm của AB và α là góc tạo bởi đường thẳng MC’ và mặt phẳng (ABC). Khi đó tanα bằng
A. 2 7 7 .
B. 3 2 .
C. 3 7 .
D. 2 3 3 .
Đáp án D
Ta có MC là hình chiếu vuông góc của MC’ lên mp (ABC)
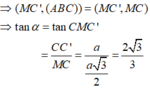
Cho hình lăng trụ đều ABC.A’B’C’có tất cả các cạnh bằng a. Gọi M là trung điểm của AB và α là góc tạo bởi đường thẳng MC’ và mặt phẳng (ABC). Khi đó tan α bằng
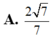
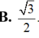
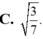
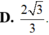
Đáp án D
Ta có MC là hình chiếu vuông góc của MC’ lên mp (ABC)
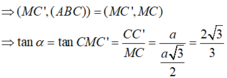
Cho hình lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M là trung điểm của AB và α là góc tạo bởi đường thẳng MC’ và mặt phẳng (ABC). Khi đó tan α bằng
A. 2 7 7 .
B. 3 2 .
C. 3 7 .
D. 2 3 3 .
Cho hình lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M là trung điểm của AB và α là góc tạo bởi đường thẳng MC’ và mặt phẳng (ABC). Khi đó tan α bằng
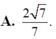
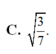
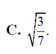

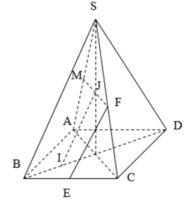
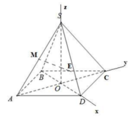
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của các cạnh BC và SA, α là góc tạo bởi đường thẳng EM và mặt phẳng S B D , tan α bằng
A. 2
B. 3
C. 2
D. 1
Đáp án A
Gọi I,J lần lượt là trung điểm cạnh BC và SA
Ta có A C ⊥ S B D , EI // AC, MJ//AC => E I ⊥ ( S B D ) , M J ⊥ ( S B D )
Suy ra, IJ là hình chiếu vuông góc của EM lên (SBD)
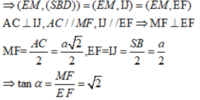
Cho lăng trụ A B C . A ' B ' C ' có đáy ABC là tam giác đều cạnh 2a, hình chiếu vuông góc của A lên mặt phẳng ( A ' B ' C ' ) là trung điểm H của A’B’. Gọi M, N lần lượt là trung điểm của A A ' , B ' C ' . Biết rằng AH = 2a và α là số đo của góc giữa đường thẳng MN và mặt phẳng ( A C ' H ) . Khi đó cos α bằng
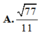
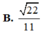
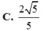
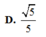
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của BC, SA, α là góc tạo bởi đường thẳng EM và mặt phẳng (SBD), tan α bằng:
A. 1
B. 2
C. 2
D. 3
Đáp án C
Phương pháp:
- Gắn hệ trục tọa độ Oxyz, tìm tọa độ các điểm E, M.
- Sử dụng công thức tính góc giữa đường thẳng và mặt phẳng: sin α = n → . u → n → . u →
Cách giải:
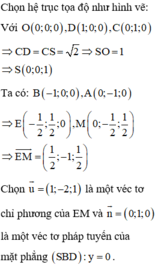
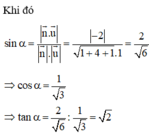
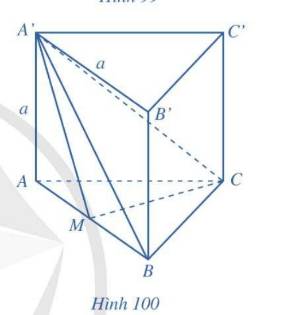
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(AB\) (Hình 100).
a) Tính góc giữa hai đường thẳng \(AB\) và \(B'C'\).
b) Tính góc giữa đường thẳng \(A'B\) và mặt phẳng \(\left( {ABC} \right)\).
c) Tính số đo của góc nhị diện \(\left[ {B,CC',M} \right]\).
d) Chứng minh rằng \(CC'\parallel \left( {ABB'A'} \right)\). Tính khoảng cách giữa đường thẳng \(CC'\) và mặt phẳng \(\left( {ABB'A'} \right)\).
e) Chứng minh rằng \(CM \bot \left( {ABB'A'} \right)\). Tính khoảng cách giữa hai đường thẳng \(CC'\) và \(A'M\).
g) Tính thể tích của khối lăng trụ tam giác đều \(ABC.A'B'C'\) và thể tích khối chóp \(A'.MBC\).
a) \(BCC'B'\) là hình chữ nhật \( \Rightarrow BC\parallel B'C'\)
\( \Rightarrow \left( {AB,B'C'} \right) = \left( {AB,BC} \right) = \widehat {ABC} = {60^ \circ }\).
b)
\(\Delta AA'B\) vuông tại \(A \Rightarrow \tan \widehat {ABA'} = \frac{{AA'}}{{AB}} = \frac{a}{a} = 1 \Rightarrow \widehat {ABA'} = {45^ \circ }\)
Vậy \(\left( {A'B,\left( {ABC} \right)} \right) = {45^ \circ }\).
c) \(CC' \bot \left( {ABC} \right) \Rightarrow CC' \bot BC,CC' \bot CM\)
Vậy \(\widehat {BCM}\) là góc nhị diện \(\left[ {B,CC',M} \right]\).
\(\Delta ABC\) đều \( \Rightarrow \widehat {BCM} = \frac{1}{2}\widehat {ACB} = {30^ \circ }\).
d) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot CM\)
\(\Delta ABC\) đều \( \Rightarrow CM \bot AB\).
\( \Rightarrow CM \bot \left( {ABB'A'} \right)\)
\(\Delta ABC\) đều \( \Rightarrow CM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\).
\(\left. \begin{array}{l}CC'\parallel AA'\\AA' \subset \left( {ABB'A'} \right)\end{array} \right\} \Rightarrow CC'\parallel \left( {ABB'A'} \right)\)
\( \Rightarrow d\left( {CC',\left( {ABB'A'} \right)} \right) = d\left( {C,\left( {ABB'A'} \right)} \right) = CM = \frac{{a\sqrt 3 }}{2}\)
e) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot CM\)
\(\Delta ABC\) đều \( \Rightarrow CM \bot AB\).
\( \Rightarrow CM \bot \left( {ABB'A'} \right) \Rightarrow CM \bot A'M\)
\(CC' \bot \left( {ABC} \right) \Rightarrow CC' \bot CM\)
\( \Rightarrow d\left( {CC',A'M} \right) = CM = \frac{{a\sqrt 3 }}{2}\)
g) \({S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4},h = AA' = a\)
\( \Rightarrow {V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.AA' = \frac{{{a^2}\sqrt 3 }}{4}.a = \frac{{{a^3}\sqrt 3 }}{4}\)
\({S_{\Delta MBC}} = \frac{1}{2}{S_{\Delta ABC}} = \frac{{{a^2}\sqrt 3 }}{8},h = AA' = a\)
\( \Rightarrow {V_{A'.MBC}} = \frac{1}{3}{S_{\Delta MBC}}.AA' = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{8}.a = \frac{{{a^3}\sqrt 3 }}{{24}}\)
Cho hình lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi α là số đo của góc hợp bởi hai mặt phẳng (AB’C) và (BCC’B’). Khi đó cosα bằng
A. 7 7
B. 2 7 7
C. 10 4
D. 3 4