Cho số phức z thỏa z - 4 + z + 4 = 10 . Giả sử m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhát z của . Tính S=m+M
A. 8
B. 16
C. 6
D. 10
Cho số phức z thỏa mãn z - 4 + 3 i - z ¯ + 4 + 3 i = 10 và z - 3 - 4 i nhỏ nhất. Môđun của số phức z bằng
A. 6
B. 7
C. 5
D. 8
Cho số phức z thỏa mãn: z - 4 + 3 i - z ¯ + 4 - 3 i = 10 và z - 3 - 4 i nhỏ nhất. Mô đun của số phức z bằng:
A. 6
B. 7
C. 5
D. 8
Cho số phức z thỏa mãn |z| = 5 và |z + 3| = |z + 3 - 10i| .Tính số phức w=z-4+3i
A. W=-4+8i
B. w=1=3i
C. w= -1+7i
D. w=-3+8i
Cho số phức z thỏa mãn |z – 4| + |z + 4| = 10. Giá trị lớn nhất và nhỏ nhất của mô – đun của số phức z là
A. 10 và 4
B. 5 và 4
C. 4 và 3
D. 5 và 3
Chọn D.
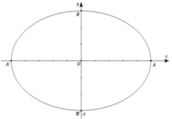
Giả sử z = x + yi có điểm biểu diễn là M(x; y).
Giả sử F1( 4 ; 0) ; F2( 0 ; -4) khi đó tập hợp các điểm M thỏa mãn là MF1+ MF2= 10 là đường elip (E) có các tiêu điểm là F1 ; F2 và trục lớn bằng 10.
Từ đó ta tìm được 2c = F1F2 = 8 nên c = 4.
2a = 10 nên a = 5
suy ra b2 = a2 - c2 = 9 nên b = 3.
Từ đó 
Vì M di động trên (E) nên |z| = OM lớn nhất, nhỏ nhất khi OM lần lượt là độ dài nửa bán trục lớn, nửa bán trục nhỏ. Hay max |z| = 5 ; min |z| = 3.
Câu 1 : Cho số phức \(z\) thỏa mãn \(z\) + ( 2 - i )\(\overline{z}\) = 3 - 5i. Môđun của số phức w = \(z \) - i bằng bao nhiêu ?
Câu 2 : Cho số phức \(z\) = a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )\(z\) + ( 2 - i )2 = 4 + i. Tính P = a - b
Cho số phức z thỏa (2i-1)z=4-3i.Tìm điểm M là điểm biểu diễn của số phức z -
A. M(2 ;1)
B. M(2 ;-1)
C. M(-2;1)
D. M(-2;-1)
Cho số phức z thỏa mãn: z ( 1 + 2 i ) - z ¯ ( 2 - 3 i ) = - 4 + 12 i . Tìm tọa độ điểm M biểu diễn số phức z.
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn \(z^4=476+480i\). Tìm z
Lời giải:
Đặt $z=a+bi$ với $a,b\in\mathbb{R}$.
$z^4=476+480i$
$\Leftrightarrow (a+bi)^4=476+480i$
$\Leftrightarrow (a^2-b^2+2abi)^2=476+480i$
$\Leftrightarrow (a^2-b^2)^2-4a^2b^2+4ab(a^2-b^2)i=476+480i$
\(\Rightarrow \left\{\begin{matrix} (a^2-b^2)^2-4a^2b^2=476\\ ab(a^2-b^2)=120\end{matrix}\right.(*)\)
Đặt $ab=x; a^2-b^2=y$ thì: \(\left\{\begin{matrix} y^2-4x^2=476\\ xy=120\end{matrix}\right. \Rightarrow \left\{\begin{matrix} y^2=4x^2+476\\ x^2y^2=14400\end{matrix}\right.\)
\(\Rightarrow x^2(4x^2+476)=14400\)
$\Rightarrow x^2=25$
$\Rightarrow x=\pm 5\Rightarrow y=\pm 24$
Nếu $x=5$ và $y=24$ thì $ab=5; a^2-b^2=24$
$\Leftrightarrow a^2(-b^2)=-25; a^2+(-b^2)=24$. Theo Viet đảo thì $a^2,-b^2$ là nghiệm của PT $X^2-24X-25=0$
$\Rightarrow a^2=25; b^2=1$. Kết hợp với $(*)$ suy ra $(a,b)=(5,1),(-5,-1)$
$\Rightarrow z=5+i$ hoặc $-5-i$
Trường hợp còn lại tương tự thì $z=\pm (1-5i)$
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + + z ) z ¯ .
A. -2
B. 0.
C. -1
D. 1
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + z ) z ¯ .
![]()
![]()
![]()
![]()