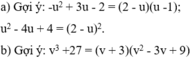Chứng minh đẳng thức: u − uv + v − v 2 v 3 − 3 v 2 + 3 v − 1 = u + v − v 2 + 2 v − 1 với v ≠ 1 .

Những câu hỏi liên quan
Bài 1: Rut gọn BT
2, u2v2(u+v)2-(u2v+uv2)2
CÁC BẠN GIÚP MK NHA ĐÂY LÀ HANG ĐẲNG THỨC ĐẮNG NHỚ NHÉ ^^
THANKS^^
u^2v^2(u+v)^2-(u^2v+uv^2)^2 - Step-by-Step Calculator - Symbolab
Tham khảo ở đó nhé!
Đúng 0
Bình luận (0)
Chứng minh các đẳng thức sau:a)
−
u
2
+
3
u
−
2
(
u
+
2
)
(
u
−
1
)
u
2...
Đọc tiếp
Chứng minh các đẳng thức sau:
a) − u 2 + 3 u − 2 ( u + 2 ) ( u − 1 ) = u 2 − 4 u + 4 4 − u 2 với u ≠ ± 2 và u ≠ 1 ;
b) v 3 + 27 v 2 − 3 v + 9 = v + 3 .
chứng minh bất đẳng thức
Cho u \(\le\) v . Chứng minh rằng u3 - 3u \(\le\)v3 - 3v + 4
Ta có :
<=> u3 - 3u - 2 \(\le\) v3 - 3v + 2 <=> ( u + 1 )2( u - 2 ) \(\le\) ( v - 1 )2( v + 2 )
Đặt x = u + 1 , y = v -1 thì :
BĐT <=> x3 - 3x2 \(\le\) y3 + 3y2 <=> x3 - y3 \(\le\) 3(x2 + y2)
Ta có : x - y = ( u - v ) + 2 \(\le\)2
=> ( x - y ) ( x2 + xy + y2 ) \(\le\)2( x2 + xy + y2) = 2(x2 + y2) + 2xy \(\le\) 2(x2 + y2) + ( x2 + y2 ) = 3(x2 + y2 ) => x3 - y3 \(\le\) 3(x2 +y2 ) ( đpcm)
Dấu bằng xảy ra khi <=> x = y = 0 <=> u = -1 ; v = 1
Đúng 0
Bình luận (0)
Chứng minh các bất đẳng thức sau:
a/ Nếu x2 + y2 = u2 + v2 thì |x(u+v) + y(u-v)| \(x <= \sqrt{2}\)
nvfbccxvxhgđggcftg;k/mk[',ươp'.kl,oklk=jtyh-
Chứng minh các bất đẳng thức sau:
a/ Nếu x2 + y2 = u2 + v2 thì |x(u+v) + y(u-v)| <=√2
\(\left|x\left(u+v\right)-y\left(u-v\right)\right|^2\le\left(x^2+y^2\right)\left[\left(u+v\right)^2+\left(u-v\right)^2\right]=1\cdot\left(2u^2+2v^2\right)=2\)
\(\Rightarrow\left|x\left(u+v\right)-y\left(u-v\right)\right|\le\sqrt{2}\)
@Hải Ngọc Cảm ơn câu trả lời của bạn, nhưng ở đoạn đầu bạn nhầm dấu cộng thành dấu trừ rồi! :))
Chứng minh đẳng thức sau với
v
≠
0
;
±
1
:
2
(
v
+
1
)
3
.
1
v
+...
Đọc tiếp
Chứng minh đẳng thức sau với v ≠ 0 ; ± 1 :
2 ( v + 1 ) 3 . 1 v + 1 + 1 v 2 + 2 v + 1 . 1 v 2 + 1 : 1 − v v 3 = v 1 − v .
Biến đổi vế trái chúng ta thu được vế phải.
Đúng 0
Bình luận (0)
viết các đẳng thức sau thành bình phương của 1 tổng hoặc hiệu :
a , 25 x mũ 2 - 10xy + y mũ 2
b , 4/9 x mũ 2 + 20/x xy + 25 y mũ 2
c , 16 uv mũ 2 - 8 u mũ 2 v mũ 4 - 1
\(25x^2-10xy+y^2=\left(5x\right)^2-2.5x.y+y^2=\left(5x-y\right)^2\)
\(\dfrac{4}{9}x^2+\dfrac{20}{3}xy+25y^2=\left(\dfrac{2}{3}x\right)^2+2.\dfrac{2}{3}x.5y+\left(5y\right)^2=\left(\dfrac{2}{3}x+5y\right)^2\)
Đúng 1
Bình luận (0)
Tìm hai số u và v trong mỗi trường hợp sau:
a) u + v = 32 , uv = 231
b) u + v = -8, uv = -105
c) u + v = 2, uv = 9
a) S = 32 ; P = 231 ⇒ S 2 – 4 P = 322 – 4 . 231 = 100 > 0
⇒ Tồn tại u và v là hai nghiệm của phương trình: x 2 – 32 x + 231 = 0 .
Ta có: Δ = ( - 32 ) 2 – 4 . 231 = 100 > 0
⇒ PT có hai nghiệm:
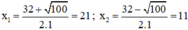
Vậy u = 21 ; v = 11 hoặc u = 11 ; v = 21.
b) S = -8; P = -105 ⇒ S 2 – 4 P = ( - 8 ) 2 – 4 . ( - 105 ) = 484 > 0
⇒ u và v là hai nghiệm của phương trình: x 2 + 8 x – 105 = 0
Ta có: Δ ’ = 4 2 – 1 . ( - 105 ) = 121 > 0
Phương trình có hai nghiệm:
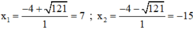
Vậy u = 7 ; v = -15 hoặc u = -15 ; v = 7.
c) S = 2 ; P = 9 ⇒ S 2 – 4 P = 2 2 – 4 . 9 = - 32 < 0
⇒ Không tồn tại u và v thỏa mãn.
Đúng 0
Bình luận (0)
Tìm 2 số u và v trong mỗi trường hợp sau:
a, u+v=32, uv=231, b,u+v=-8, uv=-105, c, u+v=2, uv=9
Tức là như thế này:
a/ \(u+v=32\Rightarrow u=32-v\)hoặc \(v=32-u\)(Cái này tùy bạn chọn nhưng mình chọn cái 1)
Ta có: \(uv=231\)
\(\Leftrightarrow\left(32-v\right)v=231\)
\(\Leftrightarrow32v-v^2-231=0\)
\(\Leftrightarrow-v^2+32v-231=0\)
Sau đó bạn giải \(\Delta\)tìm được \(v\)và có \(v\)rồi thì ra cái còn lại.
Các câu sau tương tự không có gì hết
Đúng 0
Bình luận (0)
a) từ tổng u+v=32 => u=32-v rồi thay u=32-v vào uv=231 sẽ tìm ra u;v
các câu sau làm tương tự
Đúng 0
Bình luận (0)
Xem thêm câu trả lời