Tính thể tích của hình hộp ABCD.A'B'C'D' biết rằng AA'B'D' là tứ diện đều cạnh bằng a.

A. a 3 2 2
B. a 3 2 4
C. a 3 3 2
D. a 3 2
Tính thể tích của hình hộp ABCDA'B'C'D' biết rằng AA'B'D' là tứ diện đều cạnh bằng a.
A. a 3 2 2
B. a 3 2 4
C. V = a 3 3 2
D.
Biết rằng khối tứ diện đều cạnh bằng k thì có thể tích bằng 2 k 3 12 . Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a 2 . Tính theo a thể tích khối tứ diện A C B ' D ' .
A. 2 2 a 3 3
B. 2 a 3 6
C. 2 a 3 2
D. a 3 3
Chọn đáp án A.

Chú ý: Tứ diện đều chỉ là trường hợp đặc biệt của một số tứ diện hoặc một hình chóp tam giác. Chúng ta có các kết quả như sau:
1. Cho khối chóp tam giác đều có cạnh đáy bằng a và cạnh bên bằng b. Thể tích khối chóp tam giác đều bằng
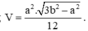
2. Cho khối tứ diện ABCD có và các cạnh còn lại đều bằng a. Thể tích khối tứ diện ABCD là ![]()
3. Cho khối tứ diện ABCD có AB = x, CD = y và các cạnh còn lại đều bằng a. Thể tích khối tứ diện ABCD là
![]()
4. Cho khối tứ diện gần đều ABCD có AB = CD = a, AC = BD = b, AD = BC = c. Thể tích khối tứ diện ABCD là
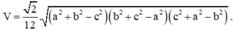
Tính thể tích của hình hộp ABCDA'B'C'D' biết rằngAA'B'D' là tứ diện đều cạnh bằng a.
A. a 3 2 2
B. a 3 2 4
C. a 3 3 2
D. a 3 2
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=a, AA'=2a Biết thể tích hình cầu ngoại tiếp tứ diện ABCD' là 9 π a 3 2 Tính thể tích V của hình hộp chữ nhật ABCD.A'B'C'D'.
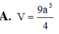
![]()
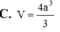
![]()
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AA' = 2a. Biết thể tích hình cầu ngoại tiếp tứ diện ABCD' là 9 πa 3 2 . Tính thể tích V của hình hộp chữ nhật ABCD.A'B'C'D'.
A. V = 9 a 3 4
B. V = 4 a 3
C. V = 4 a 3 3
D. V = 2 a 3
Đáp án B
Thể tích khối cầu ngoại tiếp tứ diện ABCD’ chính là thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.A’B’C’D’. Khi đó, bán kính khối cầu ngoại tiếp là R = A C ' 2 .
Ta có V = 4 3 πR 3 = 4 3 π . AC ' 3 8 = 9 2 πa 3 ⇒ AC ' 3 = 27 a 3 ⇒ AC ' = 3 a .
Mặt khác A C ' 2 = A B 2 + A D 2 + A A ' 2 ⇒ A D 2 = ( 3 a 2 ) - a 2 - ( 2 a ) 2 = 4 a 2 ⇒ A D = 2 a .
Vậy thể tích của hình hộp chữ nhật ABCD.A'B'C'D' là V = A A ' . A B . A D = a . 2 a . 2 a = 4 a 3 .
Bài1 :Cho hình hộp chữ nhật ABCD.A'B'C'D' , AB = 10cm , AA' = 15cm , BC= 20cm
a, Tính thể tích hình hộp chữ nhật
b, Tính AC'
Bài 2 : Cho hình chóp tứ giác đều S.ABCD có đáy AB = 10 cm , cạnh bên SA = 12 cm
a, Đường cao SO của chóp ?
b, Tính thể tích của chóp .
Bài 3 : Diện tích 3 mặt của hình hộp chữ nhật là 30cm2 , 40cm2, 75cm2 . Hỏi thể tích của hình hộp chữ nhật đó bằng bao nhiêu km3
Bài 4 : Cho hình chóp tứ giác đều S.ABCD có chiều cao SH = 3 cm , thể tích của chóp bằng 16 cm3
a , Tính độ dài cạnh đáy của chóp
b , Tính diện tích xung quanh của chóp
Hình hộp ABCD.A'B'C'D' có các cạnh đều bằng a. Tính thể tích V của hình hộp đó biết B A D ^ = D A A ' ^ = B A A ' ^ = 60 °
A. V = a 3 6
B. V = a 3 3 12
C. V = a 3 3
D. V = a 3 2 2
Đáp án D
Có A'.ABD là tứ diện đều cạnh a có 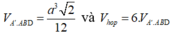
Cho hình hộp đứng A B C D . A ' B ' C ' D ' có tất cả các cạnh đều bằng a, A B C ^ = 45 0 . Tính thể tích V của khối hộp A B C D . A ' B ' C ' D ' .
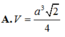
![]()
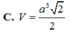
![]()
Cho hình lăng trụ \(ABCD.A'B'C'D'\). Biết \(A'.ABCD\) là hình chóp đều có tất cả các cạnh đều bằng nhau và bằng \(a\). Tính theo \(a\) thể tích của khối lăng trụ \(ABCD.A'B'C'D'\) và thể tích của khối chóp \(A'.BB'C'C\).
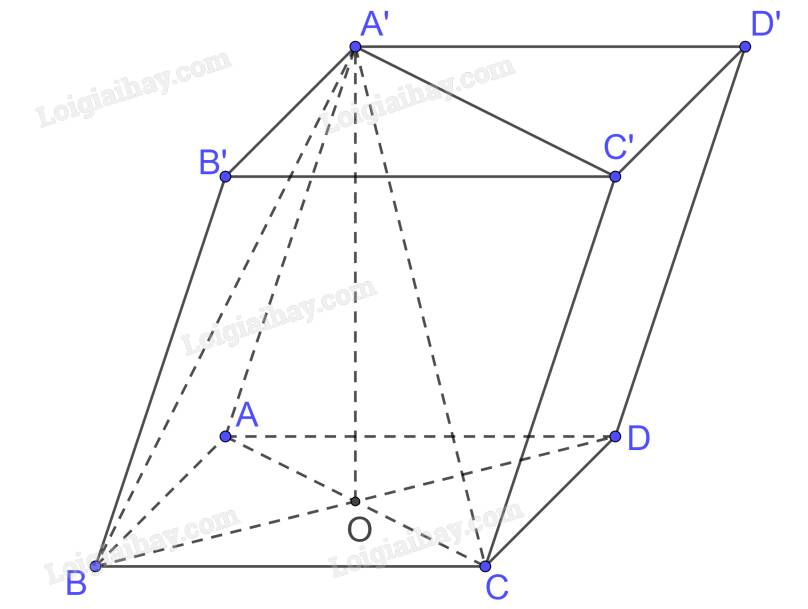
Gọi \(AC \cap BD = \left\{ O \right\}\) mà A’.ABCD là hình chóp đều nên \(A'O \bot \left( {ABCD} \right)\)
Xét tam giác ABC vuông tại B có \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\( \Rightarrow OA = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác A’AO vuông tại O có
\(A'O = \sqrt {A{{A'}^2} - A{O^2}} = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{{a\sqrt 2 }}{2}\)
\({S_{ABCD}} = {a^2}\)
Vậy khối lăng trụ có thể tích \(V = \frac{1}{3}A'O.{S_{ABCD}} = \frac{1}{3}.\frac{{a\sqrt 2 }}{2}.{a^2} = \frac{{{a^3}\sqrt 2 }}{6}\)
Nếu hình lăng trụ \(ABCD.A'B'C'D'\) xoay lại thành hình lăng trụ AA’D’D.BB’C’C thì thể tích không thay đổi do đó thể tích hình chóp \(A'.BB'C'C\) bằng một phần 3 thể tích hình lăng trụ AA’D’D.BB’C’C vì chung đáy và chung chiều cao kẻ từ A’ xuống đáy BB’C’C.
Thể tích khối chóp là \({V_{A'.BB'C'C}} = \frac{1}{3}.\frac{{{a^3}\sqrt 2 }}{6} = \frac{{{a^3}\sqrt 2 }}{{18}}\)