Giao điểm của hai đường thẳng x + y - 5 = 0 và 2x - 3y + 5 = 0 có tọa độ là
A. (2;3)
B. (1;1)
C. (-2;-3)
D. (4;1)
Giao điểm của hai đường thẳng x + y - 5 = 0 và 2x - 3y - 15 = 0 có tọa độ là:
A. (2;3)
B. (6;-1)
C. (1;4)
D. (6;1)
Chọn B.
Tọa độ giao điểm là nghiệm của hệ phương trình:
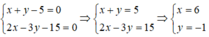
Tìm tọa độ giao điểm của đường thẳng ( a) : 4x- y-5= 0 và đường thẳng (b) : 2x- 3y – 5= 0.
A. (1; 1)
B. Không có giao điểm.
C. (1; -1)
D. Có vô số điểm chung
Gọi M( x; y) là giao điểm của 2 đường thẳng (a) và (b) ( nếu có).
Khi đó; tọa độ điểm M là nghiệm hệ phương trình:
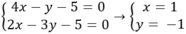
Vậy tọa độ giao điểm của 2 đường thẳng đã cho là : M( 1; -1)
Chọn C.
Trong mặt phẳng tọa độ Oxy cho điểm M(1,-1)và hai đường thẳng có phương trình (d1):x - y - 1 = 0 và (d2) 2x+y-5=0. Gọi A là giao điểm của 2 đường thẳng trên . Biết rằng có 2 đường thẳng (d) đi qua M cắt 2 đường thẳng trên tại B,C sao cho tam giác ABC có BC=3AB .Tìm phương trình đường thẳng của 2 đường thẳng đó
Tìm tọa độ giao điểm của đường thẳng (d) : 2x- 3y+ 12= 0 và đường thẳng y= 2
A. (2; 2)
B. (-3; 2)
C. (3; 2)
D. ( 2; 3)
Gọi M( x; y) là giao điểm của đường thẳng (d) và đường thẳng y= 2
Khi đó; tọa độ điểm M là nghiệm hệ phương trình:
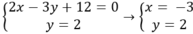
Vậy M( - 3; 2)
Chọn B.
Lập phương trình của đường thẳng ∆ đi qua giao điểm của hai đường thẳng d1: x + 3y – 1 =0 d2: x – 3y - 5= 0 và vuông góc với đường thẳng d3: 2x - y + 7 = 0.
A. 3x + 6y - 5=0.
B. 6x + 12y - 5 = 0.
C. 6x+ 12y + 10 = 0.
D. x +2y + 10 = 0.
1:cho hai điểm A(1;-4); B(1;2) viết pttq đường trung trực AB
2: cho tam giác ABC có A(1; 1); B(0; -2); C( 4;2). Viết phương trình tổng quát TRUNG TUYẾN CM
3: tìm tọa độ giao điểm của hai đường thẳng sau đây: \(\Delta1:\left\{{}\begin{matrix}x=22+2t\\y=55+5t\end{matrix}\right.\)và \(\Delta2:2x+3y-19=0\)
4:cho 4 điểm A(1; 2); B(-1; 4) C(2;2 ); D(-3; 2). Tìm tọa độ giao điểm của hai đường thẳng AB và CD
5: cho M(1;2) và đường thẳng d: 2x+y-5=0. Tìm tọa độ của điểm đối xứng với điểm M qua d là?
a.viết pt đường thẳng (d) biết đường thẳng (d) đi qua điểm N(2;3) và song song với đường thẳng y=2x-5
b.tìm tọa độ giao điểm của đồ thị hàm số y=x\(^2\) và y=2x+3
c.gọi \(x_1;x_2\) là nghiệm của phương trình x\(^2\)+2x-5=0. tính A=\(\left(x_1-x_2\right)^2+x_1x_2\)
a, Cho pt đt (d) có dạng y = ax + b
(d) đi qua N(2;3) => 3 = 2a + b
(d) // y = 2x - 5 <=> \(\left\{{}\begin{matrix}a=2\\b\ne-5\end{matrix}\right.\)
Thay a = 2 ta được : 3 = 4 + b => b = -1 (tmđk )
Vậy ptđt (d) có dạng y = 2x - 1
b, Hoành độ giao điểm tm pt
\(x^2-2x-3=0\)ta có : a - b + c = 0
Vậy pt có 2 nghiệm \(x_1=-1;x_2=3\)
Với x = -1 => y = 1
Với x = 3 => y = 9
Vậy A(-1;1) ; B(3;9)
c, Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=-5\end{matrix}\right.\)
Ta có : \(A=\left(x_1+x_2\right)^2-3x_1x_2\)
Thay vào ta được :
\(A=4-3\left(-5\right)=19\)
trong mặt phẳng tọa độ Oxy,cho hai đường thẳng d1:2x-y+5=0,d2:3x+6y-1=0 và điểm P(-2,0).Gọi A là giao điểm của d1 và d2.Khi đó đường thẳng d đi qua P và cùng với d1,d2 tạo thành một tam giác cân đỉnh A có phương trình là?
Gọi \(M\left(x;y\right)\) là điểm cách đều \(d_1\) và \(d_2\)
\(\Rightarrow\dfrac{\left|2x-y+5\right|}{\sqrt{2^2+\left(-1\right)^2}}=\dfrac{\left|3x+6y-1\right|}{\sqrt{3^2+6^2}}\)
\(\Leftrightarrow\left|6x-3y+15\right|=\left|3x+6y-1\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-9y+16=0\\9x+3y+14=0\end{matrix}\right.\)
\(\Rightarrow\) Phương trình đường thẳng cần tìm có dạng:
\(\left[{}\begin{matrix}9\left(x+2\right)+3\left(y-0\right)=0\\3\left(x+2\right)-9\left(y-0\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+y+6=0\\x-3y+2=0\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn
Gọi A là giao điểm của hai đường thẳng y = x + 2 và y = 2x + 1 , tìm tọa độ của A?
A.
A(1; -3)
B.
A(3; 1)
C.
A(1; 3)
D.
A(0; 2)