a. Tìm y:
210 : y = 14,92 – 6,52
b. Tính giá trị biểu thức:
23 + 21,8 x 2.5
1.Tính giá trị của biểu thức: A=6x3−3x2+2|x|+4A=6x3−3x2+2|x|+4 với x=−23
2.Tính giá trị của biểu thức: B=2|x|−3|y|B=2|x|−3|y| với x=12;y=−3x=12;y=−3.
3.Tìm x, biết: |2 + 3x| = |4x - 3|
1. A = 6x^3 - 3x^2 + 2.|x| + 4 với x = -23
Thay x = -23 vào biểu thức trên, ta có:
A = 6.(-23)^3 - 3.(-23)^2 + 2.|-23| + 4
A = -74539
2. B = 2.|x| - 3.|y| với x = 12; y = -3
Thay x = 12; y = -3 vào biểu thức trên, ta có:
B = 2.|12| - 3.|-3|
B = 15
3. |2 + 3x| = |4x - 3|
ta có: 2 + 3x = \(\hept{\begin{cases}4x-3\Leftrightarrow4x-3\ge0\Leftrightarrow x\ge\frac{3}{4}\\-\left(4x-3\right)\Leftrightarrow4x-3< 0\Leftrightarrow x< \frac{3}{4}\end{cases}}\)
Nếu x >= 3/4, ta có phương trình:
2 + 3x = 4x - 3
<=> 3x - 4x = -3 - 2
<=> -x = 5
<=> x = 5 (TM)
Nếu x < 3/4, ta có phương trình:
2 + 3x = -(4x - 3)
<=> 2 + 3x = -4x + 3
<=> 3x + 4x = 3 - 2
<=> 7x = 1
<=> x = 1/7 (TM)
Vậy: tập nghiệm của phương trình là: S = {5; 1/7}
Cho x,y,z là các số nguyên thoả (x-y)^3 + (y-z)^3 + (z-x)^3=210 và x-y, y-z, z-x đều khác +-1. Tính giá trị của biểu thức A= |x-y| + |y-z| + |z-x|
a. Tìm giá trị của $x$ sao cho biểu thức $A = x - 1$ có giá trị dương.
b. Đưa thừa số ra ngoài dấu căn, tính giá trị biểu thức $B = 2\sqrt{2^2.5} - 3\sqrt{3^2.5} + 4\sqrt{4^2.5}$.
c. Rút gọn biểu thức $C = \left(\dfrac{1-a\sqrt a}{1-\sqrt a} + \sqrt a\right) \left(\dfrac{1-\sqrt a}{1-a}\right)^2 $ với $a \ge 0$ và $a \ne 1$.
a, Để A nhận giá trị dương thì \(A>0\)hay \(x-1>0\Leftrightarrow x>1\)
b, \(B=2\sqrt{2^2.5}-3\sqrt{3^2.5}+4\sqrt{4^2.5}\)
\(=4\sqrt{5}-9\sqrt{5}+16\sqrt{5}=\left(4-9+16\right)\sqrt{5}=11\sqrt{5}\)
( theo công thức \(A\sqrt{B}=\sqrt{A^2B}\))
c, Với \(a\ge0;a\ne1\)
\(C=\left(\frac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\frac{1-\sqrt{a}}{1-a}\right)^2\)
\(=\left(\frac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)}{1-\sqrt{a}}+\sqrt{a}\right)\left(\frac{1-\sqrt{a}}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}\right)^2\)
\(=\left(\sqrt{a}+1\right)^2.\frac{1}{\left(\sqrt{a}+1\right)^2}=1\)
Tính giá trị của các biểu thức
a, x+ 123 với x=- 23
b,- 203+ y với y=16
a) x+ 123 với x= -23
-23 + 123 = 100
b) -203 + y với y= 16
-203 + 16= -187
Tính giá trị biểu thức: 7,4 x 21,8 - 56,52 : 3,6 =
Ta có: 7,4 x 21,8 - 56,52 : 3,6
= 161,32 - 15,7
= 145,62
Cho mình đúng nhé! ^^
Xét biểu thức F(x, y) = 2x + 3y với (x; y) thuộc miền tam giác OAB ở HĐ2. Toạ độ ba đình là O(0, 0), A(150, 0) và B(0; 150) (H.2.5).
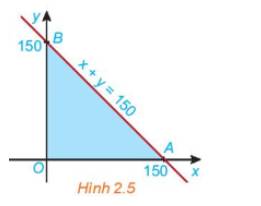
a) Tính giá trị của biểu thức F(x; y) tại mỗi đỉnh O, A và B.
b) Nêu nhận xét về dấu của hoành độ x và tung độ y của điểm (x; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị nhỏ nhất của F(x; y) trên miền tam giác OAB.
c) Nêu nhận xét về tổng x + y của điểm (X; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị lớn nhất của F(x, y) trên miền tam giác OAB.
a) Thay tọa độ điểm O, A, B vào F(x;y) ta được:
F(0;0)=2.0+3.0=0
F(150;0)=2.150+3.0=300
F(0;150)=2.0+3.150=450.
b) Lấy một điểm bất kì trong miền tam giác OAB.
Vì miền OAB là miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\) nên mọi điểm (x;y) thuộc miền OAB thỏa mãn \(x \ge 0\).
Vì miền OAB là miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\) nên mọi điểm (x;y) thuộc miền OAB thỏa mãn \(y \ge 0\).
Vậy \(x \ge 0\) và \(y \ge 0\).
=> \(F\left( {x;y} \right) = 2x + 3y \ge 2.0 + 3.0 = 0\)
Vậy giá trị nhỏ nhất của F(x;y) trên miền OAB là 0.
c) Vì miền OAB là miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\) nên mọi điểm (x;y) thuộc miền OAB thỏa mãn \(x + y \le 150\)
Như vậy với mỗi điểm trong miền tam giác OAB thì đều có tổng \(x + y \le 150\)
Quan sát miền OAB ta thấy điểm B(0;150) là điểm có tung độ lớn nhất nên mọi điểm (x;y) thuộc miền OAB đều có \(y \le 150\).
Vậy ta có: \(F\left( {x;y} \right) = 2x + 3y\)\( = 2.\left( {x + y} \right) + y\)\( \le 2.150 + 150 = 450\)
Dấu “=” xảy ra khi x+y=150 và y=150. Hay x=0, y=150.
Giá trị lớn nhất trên miền OAB là 450 tại điểm B.
Tính giá trị biểu thức:
( 375,4 x 12,5- 25,7: 2,75) x( 21,8: 0,25-43,6 x 2)
Tính máy tính ra liền ak
( 375,4 x 12,5- 25,7: 2,75) x( 21,8: 0,25-43,6 x 2)=0
Chúc bạn hok tốt!!!
( 375,4 x 12,5- 25,7: 2,75) x( 21,8: 0,25-43,6 x 2)
= ( 375,4 x 12,5- 25,7: 2,75) x( 87,2 - 87,2)
= ( 375,4 x 12,5- 25,7: 2,75) x 0
= 0
~ HOK TỐT ~
Tính giá trị biểu thức:
a) A = 15 x 5 y 3 : 10 xy 2 tại x = -3 và y = 2 3 ;
b) B = - ( x 3 y 5 z 2 ) 2 : ( - x 2 y 3 z ) 3 tại x = l,y = - 1 và z = 100.
a) Rút gọn được A = 3 2 x 4 y . Thay x = − 3 ; y = 2 3 vào A ta tìm được A = 81.
b) Rút gọn được B = yz. Thay x = 1; y = -1; z = 100 vào B ta tìm được B = -100.
Tính giá trị biểu thức:
a) M = ( - 2 x 2 y 2 + 4 xy - 6 xy 3 ) 4 : 2 3 xy tại x = 1 2 ;y = 4;
b) N = 1 3 x 2 y 5 − 2 3 x 5 y 2 : 2 x 2 y 2 tại x = -3; y = 3.
a) Kết quả M = -144. b) Kết quả N = 27 2 .