Giá trị lớn nhất và nhỏ nhất của hàm số y = 5 x + 5 1 - x trên đoạn [0;1] là:
A. m i n 0 ; 1 y = 2 5 ; m a x 0 ; 1 y = 6
B. m i n 0 ; 1 y = 2 5 ; m a x 0 ; 1 y = 5
C. m i n 0 ; 1 y = 2 ; m a x 0 ; 1 y = 6
D. m i n 0 ; 1 y = 2 ; m a x 0 ; 1 y = 5
tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bạc hai y = -2x2 + 4x + 3
tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bậc hai y = -3x2 + 2x + 1 trên (1;3)
tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bậc hai y = x2 - 4x - 5 trên (-1;4)
Câu 1:
$y=-2x^2+4x+3=5-2(x^2-2x+1)=5-2(x-1)^2$
Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $y=5-2(x-1)^2\leq 5$
Vậy $y_{\max}=5$ khi $x=1$
Hàm số không có min.
Câu 2:
Hàm số $y$ có $a=-3<0; b=2, c=1$ nên đths có trục đối xứng $x=\frac{-b}{2a}=\frac{1}{3}$
Lập BTT ta thấy hàm số đồng biến trên $(-\infty; \frac{1}{3})$ và nghịch biến trên $(\frac{1}{3}; +\infty)$
Với $x\in (1;3)$ thì hàm luôn nghịch biến
$\Rightarrow f(3)< y< f(1)$ với mọi $x\in (1;3)$
$\Rightarrow$ hàm không có min, max.
Câu 3:
$y=x^2-4x-5$ có $a=1>0, b=-4; c=-5$ có trục đối xứng $x=\frac{-b}{2a}=2$
Do $a>0$ nên hàm nghịch biến trên $(-\infty;2)$ và đồng biến trên $(2;+\infty)$
Với $x\in (-1;4)$ vẽ BTT ta thu được $y_{\min}=f(2)=-9$
Cho hàm số y = x + 1 x - 1 . Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số trên đoạn [-5;-1]. Tính M + m
A. -6
B. 2 3
C. 3 2
D. 6 5
Đáp án B
Phương pháp:
Phương pháp tìm GTLN, GTNN của hàm số y = f(x) trên [a;b]
+) Bước 1: Tính y’, giải phương trình y' = 0 ⇒ xi ∈ [a;b]
+) Bước 2: Tính các giá trị f(a); f(b); f(xi)
+) Bước 3:


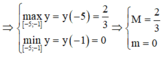
![]()
Cho hàm số y = x + 1 x - 1 . Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số trên đoạn [-5;-1]. Tính M+m
A. -6
B. 2 3
C. 3 2
D. 6 5
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số :
a. y=\(\sqrt{\text{3(1+ sin(x))}}\)-5
b. y= 6 sin(x+8)-5
Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
y = (x + 1)/(x - 1) trên đoạn [3; 5].
y ' = - 2 x - 1 2 < 0 trên đoạn [3; 5]. Vậy hàm số nghịch biến trên đoạn [3; 5].
Khi đó trên đoạn [-3,5]: hàm số đạt giá trị lớn nhất tại x = 3 và giá trị lớn nhất bằng 2, hàm số đạt giá trị nhỏ nhất tại x = 5 và giá trị nhỏ nhất = 1.5.
Tính giá trị lớn nhất và nhỏ nhất của hàm số:
y = 5 - 4 x trên đoạn [-1 ; 1].
TXĐ: D = (-∞; 5/4]
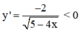 với ∀ x ∈ (-∞; 5/4)
với ∀ x ∈ (-∞; 5/4)
⇒ Hàm số nghịch biến trên (-∞; 5/4)
⇒ Hàm số nghịch biến trên [-1; 1]
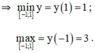
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số y = 5 - 2 cos 2 x sin 2 x
5 - 2 cos 2 x . sin 2 x = 5 - sin 2 2 x 2
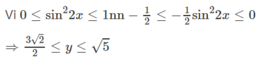
S u y r a g i á t r ị l ớ n n h ấ t c ủ a y = 5 t ạ i x = k π / 2 , g i á t r ị n h ỏ n h ấ t l à
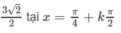
Cho hàm số y=f(x) = 4x^2+ 6x-5 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×). b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-6}{2\cdot4}=\dfrac{-6}{8}=\dfrac{-3}{4}\\y=-\dfrac{6^2-4\cdot4\cdot\left(-5\right)}{4\cdot4}=-\dfrac{29}{4}\end{matrix}\right.\)
Bảng biến thiên là:
| x | -\(\infty\) -3/4 +\(\infty\) |
| y | -\(\infty\) -29/4 +\(\infty\) |

b: Hàm số đồng biến khi x>-3/4; nghịch biến khi x<-3/4
GTNN của hàm số là y=-29/4 khi x=-3/4
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = 3sin2x – 5 lần lượt là
A. – 8 và - 2
B. 2 và 8
C. – 5 và 2
D. – 5 và 3
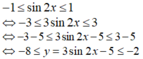
Vậy giá trị nhỏ nhất và giá trị lớn nhất của hàm số đã cho là - 8 và – 2.
Đáp án A
Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) y = x2 trên đoạn [-3; 0];
b) y = trên đoạn [3; 5].