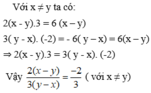Chứng minh đẳng thức sau: x 2 y + 2 x y 2 + y 3 2 x 2 + x y - y 2 = x y + y 2 2 x - y

Những câu hỏi liên quan
chứng minh đẳng thức sau: (x+y)(x+y+z)-2(x-1)(y+1)+2=x^2+y^2
BĐVT ta đc:\(\left(x+y\right)\left(x+y+z\right)-2\left(x-1\right)\left(y+1\right)+2\)
\(=x^2+2xy+y^2+xz+yz-\left[\left(2x-1\right)\left(y+1\right)\right]\)
\(=x^2+2xy+y^2+xz+yz-\left(2xy+2x-y-1\right)\)
\(=x^2+y^2+2xy+xz+yz-2xy-2x+y+1\)
Đề sai hả bn
Đúng 0
Bình luận (0)
mik phân tích đc như này:
x^2+xy+yx+y^2+xz+yz-(2x+2)(y+1)+2=x^2+y^2
Đúng 0
Bình luận (0)
chứng minh đẳng thức sau: (x+y)(x+y+z)-2(x-1)(y+1)+2=x^2+y^2
chứng minh các đẳng thức sau
(x+y)2+(x-y)2=2(x2+y2)
\(\left(x+y\right)^2+\left(x-y\right)^2=2\left(x^2+y^2\right)\)
\(\Leftrightarrow x^2+2xy+y^2+x^2-2xy=2\left(x^2+y^2\right)\)
\(\Leftrightarrow2x^2+2y^2=2\left(x^2+y^2\right)\left(đúng\right)\)
Đúng 1
Bình luận (0)
chứng minh các đẳng thức sau
(x+y)2+(x-y)2=2(x2+y2)
chứng minh biểu thức sau không phụ thuộc x
N=(x-5)(x+2)+3(x-2)(x+2)-(3x-\(\dfrac{1}{2}\)x2)+5x2
chứng minh đẳng thức sau là đẳng thức đúng
(y-1)(y2+y+1)=y3-1
a) \(N=\left(x-5\right)\left(x+2\right)+3\left(x-2\right)\left(x+2\right)-\left(3x-\dfrac{1}{2}x^2\right)+5x^2\)
\(=x^2+2x-5x-10+3x^2-12-3x+\dfrac{1}{2}x^2+5x^2\)
\(=\dfrac{19}{2}x^2-6x-22\)
Vậy biểu thức trên phụ thuộc vào biến x.
b) \(\left(y-1\right)\left(y^2+y+1\right)=y^3-1\)
Giải:
VT = \(\left(y-1\right)\left(y^2+y+1\right)\)
\(=y^3+y^2+y-y^2-y-1\)
\(=y^3-1\)
Vậy \(\left(y-1\right)\left(y^2+y+1\right)=y^3-1\).
Đúng 0
Bình luận (0)
Giải:
a) \(N=\left(x-5\right)\left(x+2\right)+3\left(x-2\right)\left(x+2\right)-\left(3x-\dfrac{1}{2}x^2\right)+5x^2\)
\(\Leftrightarrow N=x^2-3x-10+3\left(x^2-4\right)-3x+\dfrac{1}{2}x^2+5x^2\)
\(\Leftrightarrow N=x^2-3x-10+3x^2-12x-3x+\dfrac{1}{2}x^2+5x^2\)
\(\Leftrightarrow N=-10-18x+\dfrac{19}{2}x^2\)
Vậy biểu thức trên phụ thuộc vào biễn x
b) \(\left(y-1\right)\left(y^2+y+1\right)\)
\(=y^3-y^2+y^2-y+y-1\)
\(=y^3-\left(y^2-y^2\right)-\left(y-y\right)-1\)
\(=y^3-1\)
Vậy ...
Đúng 0
Bình luận (1)
chứng minh đẳng thức sau: (x+y)(x+y+z)-2(x-1)(y+1)+2=x^2+y^2
chứng minh các đẳng thức sau (x-y)^3 +4y(2x^2+y^2)=(x+y)^3+2y(x^2+y^2)
\(\left(x-y\right)^3+4y\left(2x^2+y^2\right)=\left(x+y\right)^3+2y\left(x^2+y^2\right)\)
\(\Leftrightarrow x^3-3x^2y+3xy^2-y^3+8x^2y+4y^3=x^3+3x^2y+3xy^2+y^3+2x^2y+2y^3\)
\(\Leftrightarrow\left(-3x^2y+8x^2y\right)+3xy^2+3y^3=\left(3x^2y+2x^2y\right)+3xy^2+3y^2\)
\(\Leftrightarrow5x^2y+3xy^2+3y^2=5x^2y+3xy^2+3y^2\)
Đúng 0
Bình luận (0)
Chứng minh các đẳng thức sau: 2 ( x - y ) 3 ( y - x ) = - 2 3 ( v ớ i x ≠ y )
Chứng minh đẳng thức sau:
x(x-y)-y(y-x)=x2-y2
#Giải:
Biến đổi vế trái:
Vế trái:x(x-y)-y(y-x)
=x2-xy-(y2-xy)
=x2-xy-y2+xy
=(xy-xy)+x2-y2
Vế trái=x2-y2=Vế phải
Vậy:x(x-y)-y(y-x)=x2-y2.
Đúng 0
Bình luận (0)
Ta có:
\(x.\left(x-y\right)-y.\left(y-x\right)=x^2-xy-y^2+xy=x^2-y^2\)
Vậy \(x.\left(x-y\right)-y.\left(y-x\right)=x^2-y^2\) (đpcm)
Chúc bạn học tốt!!!
Đúng 0
Bình luận (0)
Chứng minh các đẳng thức sau
a)(a-b)2=(a+b)2-4ab
b)(x+y)2+(x-y)2=2(x2+y2)
a) Ta có:
\(VT=\left(a-b\right)^2\)
\(=a^2-2ab+b^2\)
\(=a^2+2ab+b^2-4ab\)
\(=\left(a+b\right)^2-4ab=VP\left(dpcm\right)\)
b) Ta có:
\(VT=\left(x+y\right)^2+\left(x-y\right)^2\)
\(=x^2+2xy+y^2+x^2-2xy+y^2\)
\(=\left(x^2+y^2\right)+\left(x^2+y^2\right)\)
\(=2\left(x^2+y^2\right)=VP\left(dpcm\right)\)
Đúng 1
Bình luận (1)