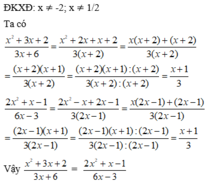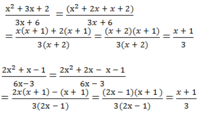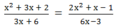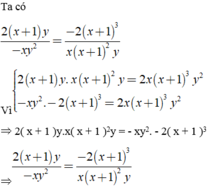Chứng minh các cặp phân thức sau bằng nhau 3 x 2 - 3 x y 3 ( x - y ) 2 và x x - y

Những câu hỏi liên quan
Dùng tính chất cơ bản của phân thức chứng minh cặp phân thức sau bằng nhau
x
2
+
3
x
+
2
3
x
+
6
và
2
x
2
+
x
-
1
6
x...
Đọc tiếp
Dùng tính chất cơ bản của phân thức chứng minh cặp phân thức sau bằng nhau x 2 + 3 x + 2 3 x + 6 và 2 x 2 + x - 1 6 x - 3
Dùng tính chất cơ bản của phân thức chứng tỏ rằng các cặp phân thức sau bằng nhau:
x
2
+
3
x
+
2
3
x
+
6
v
à
2
x
2
+...
Đọc tiếp
Dùng tính chất cơ bản của phân thức chứng tỏ rằng các cặp phân thức sau bằng nhau: x 2 + 3 x + 2 3 x + 6 v à 2 x 2 + x - 1 6 x - 3
Chứng minh các phân thức sau bằng nhau
2
(
x
+
1
)
y
-
x
y
2
-
2
(
x
+
1
)
3...
Đọc tiếp
Chứng minh các phân thức sau bằng nhau 2 ( x + 1 ) y - x y 2 = - 2 ( x + 1 ) 3 x ( x + 1 ) 2 y
Chứng minh các phân thức sau bằng nhau
2
(
x
+
1
)
y
-
x
y
2
-
2
(
x
+
1
)
3...
Đọc tiếp
Chứng minh các phân thức sau bằng nhau 2 ( x + 1 ) y - x y 2 = - 2 ( x + 1 ) 3 x ( x + 1 ) 2 y
Từ đẳng thức 2 x 3 = 1 ×6 ta có thể lập đc các cặp phân số bằng nhau như sau:2/1=6/3;. 3/1=6/2. 1/2=6/3:. 1/3=2/6. Hãy lập các cặp phân số bằng nhau từ đẳng thức 3×4=6×2
Lời giải:
$\frac{3}{6}=\frac{2}{4}$
$\frac{6}{3}=\frac{4}{2}$
$\frac{3}{2}=\frac{6}{4}$
$\frac{2}{3}=\frac{4}{6}$
Đúng 5
Bình luận (0)
Các cặp phân số bằng nhau từ đẳng thức \(3\times4=6\times2\) là:
\(\dfrac{3}{6}=\dfrac{2}{4};\) \(\dfrac{4}{6}=\dfrac{2}{3};\) \(\dfrac{6}{3}=\dfrac{2}{4};\) \(\dfrac{6}{4}=\dfrac{3}{2}\)
Đúng 5
Bình luận (0)
Chứng tỏ cặp phân thức sau bằng nhau:
3
2
x
-
3
và
3
x
+
6
2
x
2
+
x
-...
Đọc tiếp
Chứng tỏ cặp phân thức sau bằng nhau:
3 2 x - 3 và 3 x + 6 2 x 2 + x - 6
- Cách 1: Dùng định nghĩa hai phân thức bằng nhau:
3(2x2 + x – 6) = 6x2 + 3x – 18
(2x – 3)(3x + 6) = 2x.(3x + 6) – 3.(3x + 6) = 6x2 + 12x – 9x – 18 = 6x2 + 3x – 18
⇒ 3(2x2 + x – 6) = (2x – 3)(3x + 6)
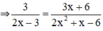
- Cách 2: Rút gọn phân thức:
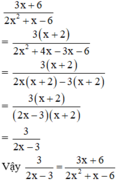
Đúng 0
Bình luận (0)
Dùng định nghĩa 2 phân thức bằng nhau chứng minh các phân thức sau bằng nhau:
\(\frac{x^2\left(x+3\right)}{x\left(x+3\right)^2}\)= \(\frac{x}{x+3}\)
Giúp Mk nha Mk tk cho 3 nk . Cần lắm những tấm lòng nhân ái
từ vế trái ta có
\(\frac{x.x\left(x+3\right)}{x.\left(x+3\right)\left(x+3\right)}\)
Rút gọn đi x và (x+3) còn
\(\frac{x}{x+3}\)
từ đó suy ra cái bên trên đó .
Đúng 0
Bình luận (0)
Xét VT, ta có: \(\frac{x^2\left(x+3\right)}{x\left(x+3\right)^2}=\frac{x}{x+3}\)= VP
Vậy ...
Đúng 0
Bình luận (0)
Đặt \(\frac{x^2\left(x+3\right)}{x\left(x+3\right)^2}=k\)\(\Rightarrow\)\(x^2\left(x+3\right)=k.x\left(x+3\right)^2\)
\(\Rightarrow\)\(\frac{k.x\left(x+3\right)^2}{x\left(x+3\right)^2}=k\)
Đặt \(\frac{x}{x+3}=k\)\(\Rightarrow\)\(x=k\left(x+3\right)\)
\(\Rightarrow\)\(\frac{k\left(x+3\right)}{x+3}=k\)
Vì\(k=k\)
Vậy \(\frac{x^2\left(x+3\right)}{x\left(x+3\right)^2}=\frac{x}{x+3}\).
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 1: Tìm điều kiện để các phân thức sau có ý nghĩa
a)5x-3/2x^2-x b)x^2-5x+6/x^2-1
c)2/(x+1)(x-3) d)2x+1/x^2-5x+6
Bài 2: Dùng định nghĩa hai phân thức bằng nhau chứng minh các đẳng thức sau:
a)x-2/-x=2^3-x^3/x(x^2+2x+4) (với x =/0)
b)3x/x+y=-3x(x+y)/y^2-x^2 (với x=/ +_ y)
c)x+y/3a=3a(x+y^2)/9a^2(x+y) (với a=/ 0,x=/-y)
Bài 1:
c: ĐKXĐ: \(x\notin\left\{-1;3\right\}\)
Đúng 0
Bình luận (0)
Bài 3: Chứng minh các phân thức sau bằng nhau
a)\(\dfrac{x+1}{x+3}\)=\(\dfrac{x^2+4x+3}{x^2+6x+9}\)
b)\(\dfrac{x+y}{3x}\)=\(\dfrac{3x\left(x+y\right)^2}{9x^2\left(x+y\right)}\)
\(a,VP=\dfrac{x^2+4x+3}{x^2+6x+9}=\dfrac{\left(x+1\right)\left(x+3\right)}{\left(x+3\right)^2}=\dfrac{x+1}{x+3}=VT\)
Vậy ta có đpcm
b, \(VP=\dfrac{3x\left(x+y\right)^2}{9x^2\left(x+y\right)}=\dfrac{x+y}{3x}=VT\)
Vậy ta có đpcm
Đúng 0
Bình luận (0)
a) Ta có: \(\dfrac{x^2+4x+3}{x^2+6x+9}\)
\(=\dfrac{\left(x+1\right)\left(x+3\right)}{\left(x+3\right)\left(x+3\right)}\)
\(=\dfrac{x+1}{x+3}\)
b: Ta có: \(\dfrac{3x\left(x+y\right)^2}{9x^2\left(x+y\right)}\)
\(=\dfrac{3x\left(x+y\right)\left(x+y\right)}{3x\cdot3x\cdot\left(x+y\right)}\)
\(=\dfrac{x+y}{3x}\)
Đúng 1
Bình luận (0)