Giải tiếp hệ (IV) bằng phương pháp đã nêu ở trường hợp thứ nhất.
(IV) 3 x + 2 y = 7 2 x + 3 y = 3
Nêu một cách khác để đưa hệ phương trình (IV) về trường hợp thứ nhất ?
(IV) 3 x + 2 y = 7 2 x + 3 y = 3
Chia cả 2 vế của phương trình thứ nhất cho 3 và 2 vế của phương trình thứ hai cho 2 ta được:
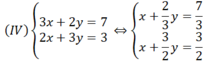
Nêu một cách khác để đưa hệ phương trình (IV) về trường hợp thứ nhất ?
Chia cả 2 vế của phương trình thứ nhất cho 3 và 2 vế của phương trình thứ hai cho 2 ta được:
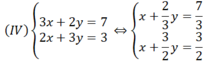
Cho hệ phương trình
(IV) 4 x + y = 2 8 x + 2 y = 1
Bằng minh họa hình học và phương pháp thế, chứng tỏ rằng hệ (IV) vô nghiệm.
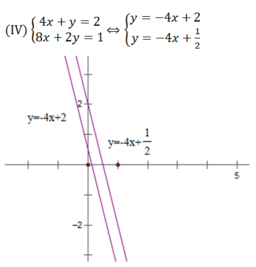
Hai đường thẳng trên song song nên chúng không có điểm chung hay hệ phương trình (IV) vô nghiệm.
Phương pháp thế:
Ta có ( biểu diễn y theo x từ phương trình thứ nhất):
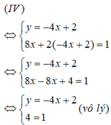
Vậy hệ phương trình (IV) vô nghiệm.
Cho hệ phương trình I V 4 x + y = 2 8 x + 2 y = 1
Bằng minh họa hình học và phương pháp thế, chứng tỏ rằng hệ (IV) vô nghiệm.
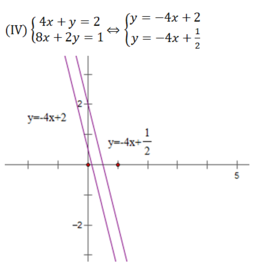
Hai đường thẳng trên song song nên chúng không có điểm chung hay hệ phương trình (IV) vô nghiệm.
Phương pháp thế:
Ta có ( biểu diễn y theo x từ phương trình thứ nhất):
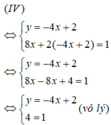
Vậy hệ phương trình (IV) vô nghiệm.
Cho hệ phương trình (IV) :
3x-y=2m-1 và x+2y=3m+2
a, Gỉai hpt ( IV) khi m=1
b, Tìm m đề hpt (IV) có nghiệm duy nhất (x;y) sao cho :x^2+y^2=5
c, Tìm m để hpt có nghiệm duy nhất x;y sao cho x-3y>0
Cho hệ phương trình (IV) :
3x-y=2m-1 và x+2y=3m+2
a, Gỉai hpt ( IV) khi m=1
b, Tìm m đề hpt (IV) có nghiệm duy nhất (x;y) sao cho :x^2+y^2=5
c, Tìm m để hpt có nghiệm duy nhất x;y sao cho x-3y>0
a) Thay \(m=1\) vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}3x-y=1\\x+2y=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Vậy ...
b) HPT \(\Leftrightarrow\left\{{}\begin{matrix}6x-2y=4m-2\\x+2y=3m+2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}7x=7m\\y=2m-1-3x\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=m\\y=-m-1\end{matrix}\right.\)
Ta có: \(x^2+y^2=5\)
\(\Rightarrow m^2+m^2+2m+1=5\) \(\Leftrightarrow m^2+m-2=0\) \(\Rightarrow\left[{}\begin{matrix}m=1\\m=-2\end{matrix}\right.\)
Vậy ...
c) Hệ phương trình luôn có nghiệm duy nhất
Ta có: \(x-3y>0\)
\(\Rightarrow m-3\left(-m-1\right)>0\)
\(\Leftrightarrow4m+3>0\) \(\Leftrightarrow m>-\dfrac{3}{4}\)
Vậy ...
Cho hệ phương trình (IV) :
3x-y=2m-1 và x+2y=3m+2
a, Gỉai hpt ( IV) khi m=1
b, Tìm m đề hpt (IV) có nghiệm duy nhất (x;y) sao cho :x^2+y^2=5
c, Tìm m để hpt có nghiệm duy nhất x;y sao cho x-3y>0
a) Thay m=1 vào hệ pt, ta được:
\(\left\{{}\begin{matrix}3x-y=1\\x+2y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-y=1\\3x+6y=15\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-7y=-14\\x+2y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=5-2y=5-2\cdot2=1\end{matrix}\right.\)
Vậy: Khi m=1 thì hệ phương trình có nghiệm duy nhất là (x,y)=(1;2)
Phả hệ sau đây mô tả sự di truyền của một bệnh hiếm gặp ở người. Biết rằng không có đột biến mới phát sinh trong phả hệ, bệnh do một trong 2 alen của một gen quy định.
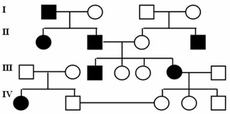

Xét các khẳng định sau đây, có bao nhiêu khẳng định đúng?
(1) Có 19 cá thể trong phả hệ đã chắc chắn được kiểu gen.
(2) Trong số các cá thể đã chắc chắn kiểu gen, có 7 cá thể có kiểu gen đồng hợp.
(3) Gen gây bệnh là gen lặn nằm tren NST giới tính X, không có alen trên Y.
(4) Xác suất để cặp vợ chồng ở thế hệ thứ IV sinh được 2 đứa con đều không bị bệnh là 17/24.
(5) Xác suất để cặp vợ chồng ở thế hệ thứ IV sinh được 2 đứa con trong đó có 1 đứa bị bệnh là 1/8.
A. 3
B. 2
C. 4
D. 1
Chọn B
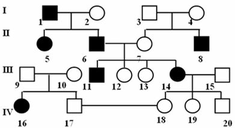

Xét cặp vợ chồng 9 x 10 :
Vợ chồng bình thường, sinh con bị bệnh
ð A bình thường >> a bị bệnh
Mà đứa con bị bệnh là con gái
ð Gen nằm trên NST thường
Những cá thể trong phả hệ biết chắc chắn được kiểu gen là :
Kiểu gen Aa có các cá thể là 2, 3, 4, 7, 12, 13, 9, 10 , 18, 19, 20
Kiểu gen aa có các cá thể là 1, 5, 6, 8, 11, 14, 16
Vậy số cá thể biết được kiểu gen là 18
Trong số các cá thể đã xảy ra chắc chắn kiểu gen (18 cá thể) các thể có kiểu gen đồng hợp là : 1, 5, 6, 8, 11, 14, 16
Vậy có 7/18 cá thể là thể đồng hợp
Cặp vợ chồng thế hệ thứ 4 : người chồng có dạng (1/3AA : 2/3Aa)
Người vợ có kiểu gen là Aa
Nếu người chồng là AA, 100% con sinh ra không bị bệnh
Nếu người chồng là Aa, xác suất sinh 2 con không bị bệnh là (3/4)2 = 9/16
Vậy xác suất chung của cặp vợ chồng này sinh 2 con không bị bệnh là
1/3 + 2/3 x 9/16 = 17/24
Để cặp vợ chồng sinh được 2 đứa con, trong đó có 1 đứa bị bệnh thì người chồng phải có kiểu gen là : Aa
Xác suất cặp vợ chồng sinh 2 đứa con, có 1 đứa bị bệnh là : ¾ x ¼ x 2 = 3/8
Vậy xác xuất cặp vợ chồng này sinh 2 đứa con, 1 đứa bị bệnh là : 2/3 x 3/8 = 1/4
Nhận định đúng là : (2) , (4)
Trong các phương pháp tạo giống cây trồng sau đây, có bao nhiêu phương pháp chắc chắn có thể tạo ra dòng thuần chủng:
I. Phương pháp nuôi cấy hạt phấn, lưỡng bội hóa.
II. Phương pháp nuôi cấy mô tế bào.
III. Phương pháp lai tế bào sinh dưỡng.
IV. Phương pháp tự thụ phấn liên tiếp qua nhiều thế hệ.
A. 4
B. 3
C. 2
D. 1
Đáp án C
I Đúng Nuôi cấy hạt phấn đơn bội, sau đó tiến hành lưỡng bội hóa sẽ tạo ra cơ thể đồng hợp tử về tất cả các cặp gen.
II Đúng Phương pháp nuôi cấy mô tế bào tạo ra các cơ thể có cùng kiểu gen, tuy nhiên kiểu gen đó có thể chứa các cặp gen dị hợp.
III Sai Tạo ra các cơ thể có các tế bào chứa bộ NST của 2 loài.
IV sai Tự thụ phấn liên tiếp qua nhiều thế hệ sẽ tạo nên dòng các dòng thuần chủng.