Chia cả 2 vế của phương trình thứ nhất cho 3 và 2 vế của phương trình thứ hai cho 2 ta được:
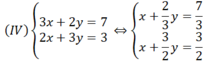
Chia cả 2 vế của phương trình thứ nhất cho 3 và 2 vế của phương trình thứ hai cho 2 ta được:
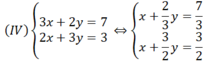
Nêu một cách khác để đưa hệ phương trình (IV) về trường hợp thứ nhất ?
Giải tiếp hệ (IV) bằng phương pháp đã nêu ở trường hợp thứ nhất.
(IV) 3 x + 2 y = 7 2 x + 3 y = 3
Cho hệ phương trình (IV) :
3x-y=2m-1 và x+2y=3m+2
a, Gỉai hpt ( IV) khi m=1
b, Tìm m đề hpt (IV) có nghiệm duy nhất (x;y) sao cho :x^2+y^2=5
c, Tìm m để hpt có nghiệm duy nhất x;y sao cho x-3y>0
Giải các hệ phương trình theo hai cách:
*Cách thứ nhất: đưa hệ phương trình về dạng: a x + b y = c a ' x + b ' y = c '
*Cách thứ hai: đặt ẩn phụ, chẳng hạn s = 3x – 2, t = 3y + 2
3 x + y - 5 x - y = 12 - 5 x + y + 2 x - y = 11
Cho hệ phương trình :
\(\left\{{}\begin{matrix}mx-y=2\\x+my=1\end{matrix}\right.\)
a) Giải hệ phương trình theo tham số m.
b) Trong trường hợp hệ phương trình có nghiệm duy nhất (x, y). Tìm các giá trị của m để x + y = -1.
Cho hệ phương trinh: 3x-my=-9. mx+2y=16
1. Tìm giá trị nguyên của m để hai đuong thẳng của hệ cắt nhau tại một điểm nằm trong góc phần tư thứ IV trên mặt phẳng toạ độ Oxy.
2. Với giá trị nguyên nào của m để hệ có nghiệm (x;y) thoả mãn x+y=7
Cho hệ phương trình : x - 2y = 3 - m và 2x + y =3(m+2). Gọi ngiệm của hệ phương trình là (x,y) .
Tìm m để x^2 +y^2 đạt giá trị nhỏ nhất
Bai3 :cho hệ phương trình: 3*x – y =1 và m*x + 2y = 3*m +2
Tìm m để hệ phương trình có nghiệm (x,y) duy nhất thõa mãn x2 +y 2 =185