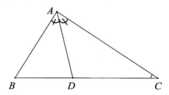
Cho tam giác ABC, tia phân giác AD (D thuộc BC). Tính A D B ^ và A D C ^ biết B ^ − C ^ = 40 °

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, kẻ tia phân giác góc ABC cắt AC tại D. Biết BC = 5cm, AB = 3cm
a) Tính AC và AD
b) Kẻ DE // AB (E thuộc BC). Tính DE
a, Theo định lí Pytago tam giác ABC vuông tại A
\(AC=\sqrt{BC^2-AB^2}=4cm\)
Vì BD là pg nên \(\dfrac{AB}{BC}=\dfrac{AD}{DC}\Rightarrow\dfrac{DC}{BC}=\dfrac{AD}{AB}\)
Theo tc dãy tỉ số bằng nhau
\(\dfrac{DC}{BC}=\dfrac{AD}{AB}=\dfrac{4}{8}=\dfrac{1}{2}\Rightarrow DC=\dfrac{5}{2}cm;AD=\dfrac{3}{2}\)cm
b, Vì DE // AB Theo hệ quả Ta lét
\(\dfrac{DC}{AC}=\dfrac{DE}{AB}\Rightarrow DE=\dfrac{AB.DC}{AC}=\dfrac{15}{8}\)cm
Đúng 1
Bình luận (0)
Cho tam giác ABC, tia phân giác AD (D thuộc BC). Tính A D B ^ và A D C ^ biết B ^ − C ^ = 40 ° .
Cho tam giác abc vuông tại A,AB=9cm,AC=12cm. Gọi BD là tia phân giác của góc ABC (D thuộc AC).Qua D kẻ DE vuông góc BC (E thuộc BC)
a)Tính độ dài BC
b)Chứng minh tam giác ABC=Tam giác EBD
c)Chứng minh AD<DC
d) gọi I là giao điểm của DE và AB.Chứng minh BIC cân
a: BC=15cm
b: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
c: Ta có: DA=DE
mà DE<DC
nên DA<DC
d: Xét ΔBEI vuông tại E và ΔBAC vuông tại A có
BE=BA
\(\widehat{EBI}\) chung
DO đó: ΔBEI=ΔBAC
Suy ra: BI=BC
hay ΔBIC cân tại B
Đúng 0
Bình luận (0)
cho tam giác abc có góc a=60độ,góc b=50 độ và ad là tia phân giác của góc bac(d thuộc bc)
a, tính góc adb
b, so sánh các cạnh của tam giác abd
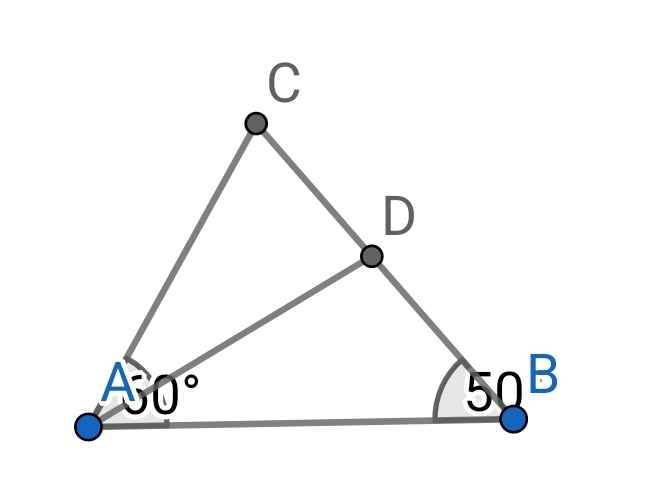 a) Do AD là tia phân giác của ∠BAC (gt)
a) Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠BAC : 2
= 60⁰ : 2
= 30⁰
∆ABD có:
∠BAD + ∠ABD + ∠ADB = 180⁰ (tổng ba góc trong ∆ABD)
⇒ ∠ADB = 180⁰ - ∠BAD - ∠ABD
= 180⁰ - 30⁰ - 50⁰
= 100⁰
b) Do 30⁰ < 50⁰ < 100⁰
⇒ ∠BAD < ∠ABD < ∠ADB
⇒ BD < AD < AB (quan hệ giữa cạnh và góc đối diện trong tam giác)
Đúng 3
Bình luận (0)
cho tam giác abc cân tại a. trên tia đối của tia ab lấy điểm d sao cho AD=AB và tia phân giác AE của CAD ( E thuộc CD ) a, vẽ tia phân giác AK của BAC ( K thuộc BC ). Chứng minh AK//CD b,Tính góc BCD
a: ΔABC cân tại A
mà AK là phân giác
nen K là trung điểm của BC
Xét ΔCBD có
A,K lần lượt là trung điểm của BD,BC
=>AK là đường trung bình
=>AK//CD
b: Xét ΔCBD có
CA là trung tuyến
CA=BD/2
=>ΔBDC vuông tại C
=>góc BCD=90 độ
Đúng 0
Bình luận (0)
cho tam giác abc cân tại a. trên tia đối của tia ab lấy điểm d sao cho AD=AB và tia phân giác AE của CAD ( E thuộc CD ) a, vẽ tia phân giác AK của BAC ( K thuộc BC ). Chứng minh AK//CD b,Tính góc BCD
a: ΔABC cân tại A
mà AK là phân giác
nen K là trung điểm của BC
Xét ΔCBD có
A,K lần lượt là trung điểm của BD,BC
=>AK là đường trung bình
=>AK//CD
b: Xét ΔCBD có
CA là trung tuyến
CA=BD/2
=>ΔBDC vuông tại C
=>góc BCD=90 độ
Đúng 0
Bình luận (0)
Cho ∆ABC vuông tại A, có AB=20cm, AC=15cm. Về đường cao AH (H thuộc BC)
a. Chứng minh: ∆HBA~∆ABC
b. Tính BC, AH, BH
c. Tia phân giác góc BAC cắt AC tại D. Tính tỉ số diện tích của 2 tam giác ABD và ACF
d. Trong ∆ABC kẻ phân giác AD (D thuộc BC). Trong ∆ADB kẻ phân giác DE (E thuộc AB) và trong ∆ADC kẻ phân giác DF (F thuộc AC). Chứng minh rằng EA/EB×DB/DC×FC/FA=1
a: Xet ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: BC=25cm
AH=15*20/25=12cm
HB=20^2/25=16cm
HC=25-16=9cm
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a có ab=6cm ac=8cm đường cao ah (h thuộc bc).kẻ d là tia phân giác bd(d thuộc ac)
a)tính ad và dc
b)chứng mnh bh/ab=ad/ac
giúp mik vớ
a) Áp dụng định lí Py-ta-go vào ΔABC vuông tại A ta có:
\(BC^2\)= \(AB^{^{ }2}\)+\(AC^2\)=\(6^2\)+\(8^2\)= 100⇒ BC=\(\sqrt{100}\)=10 (cm)
Xét ΔABC có BD là tia phân giác \(\widehat{ABC}\) ,theo t/c ta có:
\(\dfrac{AB}{BC}\)=\(\dfrac{AD}{DC}\) ⇒\(\dfrac{DC}{BC}\)=\(\dfrac{AD}{AB}\)hay \(\dfrac{DC}{10}\)=\(\dfrac{AD}{6}\)= \(\dfrac{DC+AD}{10+6}\)=\(\dfrac{AC}{16}\)=\(\dfrac{8}{16}\)=\(\dfrac{1}{2}\)
⇒\(\left\{{}\begin{matrix}AD=6.\dfrac{1}{2}=3\left(cm\right)\\DC=10.\dfrac{1}{2}=5\left(cm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A, AB = 8cm, AC = 6cm, AD là tia phân giác góc A (D thuộc BC)
a, Tính DB, DC
b, Kẻ đường cao AH (H thuộc BC) . CMR: Tam giác AHB đồng dạng tam giác CHA.
c, Tính diện tích tam giác AHB và CHA.
a) Gọi x(cm) là độ dài cạnh DB
Áp dụng định lý Pi-ta-go vào tam giác ABC vuông tại A, ta có:
BC2= AB2 + AC2= 82 + 62= 100
=>BC=\(\sqrt{100}\)=10(cm)
Xét tam giác ABC, ta có:
AD là tia phân giác góc A
=> \(\frac{DB}{AB}=\frac{DC}{AC}hay\frac{x}{8}=\frac{10-x}{6}\)
=> 6x = 8(10-x)
<=>6x=80-8x
<=>6x + 8x=80
<=> 14x=80
<=> x= 5,72(cm)
Vậy DB= 5,72 cm
DC= 10 - 5,72= 4,28 (cm)
Đúng 1
Bình luận (0)
a. tam giác ABC có góc A = 90 độ nên
BC^2=AB^2+AC^2
=8^2+6^2=100
=>BC =10
áp dụng tính chất dãy tỉ số bằng nhau ta có :
BD/AB=DC/AC =BD+DC/AB+AC=10/14=5/7
=>BD/AB=5/7=>BD=8*5:7=40/7
=>DC/Ac=5/7=>DC=6*5/7=30/7
Đúng 0
Bình luận (0)
b. Xét tam giác ABC và tam giác HAC, ta có:
góc CAB= góc CHA= 90
Góc C chung
=> Tam giac ABC đồng dạng tam giác HAC (g-g)
=> góc ABH= góc CAH
Xét tam giác AHB và tam giác CHA, ta có:
Góc AHB= góc CHA= 90
Góc ABH= góc CAH (cmt)
=> tam giác AHB đồng dạng với tam giác CHA
Đúng 0
Bình luận (0)