Cho hàm số y = x π 2 có đồ thị (C) . Lấy điểm M thuộc (C) có hoành độ x0 = 1. Hệ số góc của tiếp tuyến của (C) tại M là
A. π
B. -1
C. π 2
D. - π 2
Tìm hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm y = tanx có hoành độ x 0 = π / 4 .
câu 1: cho hàm số y=ax+b
Xác định giá trị a và b biết đồ thị hàm số đi qua điểm M; m(2;5) và N(1/3;0)
câu 2: cho hàm số:y=f(x)=-2x; g(x)=x-1
a, tính f(3); g(-2)
b, tìm tung độ của điểm A thuộc đồ thị hàm số của điểm A thuộc đồ thị hàm số f(x) có hoành độ là 1/2
c.tính hoành độ của điểm B thộc đồ thị hàm số g(x)có tung độ là -3
d, điểm C(1/3;-2/3) có thuộc đồ thị hàm số f(x); g(x) không
Xác định hệ số a, biết rằng đồ thị của hàm số y=ax đi qua điểm A(6;2).Điểm B(-9;3), điểm C(7;-2) có thuộc đồ thị hàm số không ? Tìm trên đồ thị của hàm số điểm D có hoành độ bằng -4,điểm E có tung độ bằng 2
Cho điểm A( 2;-1) thuộc đồ thị hàm số y = ax.
a) Xác định a.
b) Tìm điểm B có hoành độ là 2 và điểm C có tung độ bằng 5 thuộc đồ thị hàm số y = ax.
c) Vẽ đồ thị hàm số y =ax vừa tìm được và đồ thị hàm số y = 2x trên cùng một hệ trục tọa
độ Oxy.
d) Chứng minh 3 điểm M(-3; 1,5); N (1; -0,5) và O thẳng hàng.
LẸ GIÙM MÌNH NHA
a: Thay x=2 và y=-1 vào y=ax, ta được:
2a=-1
hay a=-1/2
Cho hàm số y = f(x). Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x 0 có hệ số góc là:
A. k = f ' x 0 . x - x 0 + f x 0
B. k = f ' x 0 + f x 0
C. k = f x 0
D. k = f ' x 0
Đáp án D
PT tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x 0 có hệ số góc k = f ' x 0 . k = f ' x 0 .
Cho hàm số y = 5 x 3 3 − x 2 + 4 có đồ thị (C). Tiếp tuyến của (C) tại điểm có hoành độ x 0 = 3 có hệ số góc là:
A. 39
B. 40
C. 51
D. 3
Đáp án A
Ta có: y ' = 5 x 2 − 2 x ; k = y ' 3 = 5.9 − 2.3 = 39.
Cho hàm số y = sin4x
a) Chứng minh rằng sin4(x + kπ/2) = sin4x với k ∈ Z
Từ đó vẽ đồ thị của hàm số
y = sin4x; (C1)
y = sin4x + 1. (C2)
b) Xác định giá trị của m để phương trình: sin4x + 1 = m (1)
- Có nghiệm
- Vô nghiệm
c) Viết phương trình tiếp tuyến của (C2) tại điểm có hoành độ x 0 = π / 24
a) Ta có sin4(x + kπ/2) = sin(4x + k2π) = sin4x với k ∈ Z.
Từ đó suy ra hàm số y = sin4x là hàm số tuần hoàn với chu kì π/2.
Vì hàm số y = sin4x là hàm số lẻ nên đồ thị của nó có tâm đối xứng là gốc tọa độ O.
Các hàm số y = sin4x (C1) và y = sin4x + 1 (C2) có đồ thị như trên hình 1 và hình 2.
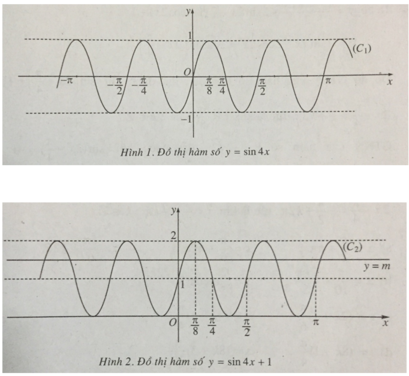
b) Vì sin4x + 1 = m ⇔ sin4x = m – 1
và -1 ≤ sin4x ≤ 1
nên -1 ≤ m – 1 ≤ 1
⇔ 0 ≤ m ≤ 2.
Từ đó, phương trình (1) có nghiệm khi 0 ≤ m ≤ 2 và vô nghiệm khi m > 2 hoặc m < 0.
c) Phương trình tiếp tuyến của (C2) có dạng
y - y o = y ’ ( x o ) ( x - x o ) .
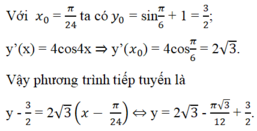
Tiếp tuyến với đồ thị hàm số y = x + 1 2 x - 3 tại điểm có hoành độ x0= -1 có hệ số góc bằng:
A. 5.
B. -1/5.
C. -5.
D. 1/5.
Tiếp tuyến với đồ thị hàm số y = x + 1 2 x - 3 tại điểm có hoành độ x 0 = - 1 có hệ số góc bằng
A. 5
B. - 1 5
C. -5
D. 1 5
Cho hàm số y=\(x^3-3x^2-1\)có đồ thị (C).Điểm M(a;b) trên(C) có hoành độ thuộc [2;3] sao cho tiếp tuyến của (C) tại M có hệ số góc lớn nhất.Khi đó, S=a+b=?
\(y'=3x^2-6x\)
Do M thuộc (C) nên hệ số góc của tiếp tuyến tại M:
\(k=f\left(a\right)=3a^2-6a\)
\(f'\left(a\right)=6a-6>0;\forall a\in\left[2;3\right]\)
\(\Rightarrow f\left(a\right)\) đồng biến trên \(\left[2;3\right]\Rightarrow k_{max}\) khi \(a=3\)
\(\Rightarrow b=a^3-3a^2-1=-1\)
\(S=3-1=2\)