Tìm tất cả các giá trị của tham số m để hệ sau có nghiệm
x 2 - 3 x + 2 ≤ 0 m x 2 - 2 ( 2 m + 1 ) x + 5 m + 3 ≥ 0
A. m > -1/2
B. m = -1/2
C. m ≥ -1/2
D. không tồn tại
Những câu hỏi liên quan
Tìm tất cả các giá trị thực của tham số m để hệ phương trình sau có nghiệm
x
2
+
4
x
+
y
m
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hệ phương trình sau có nghiệm x 2 + 4 x + y = m 2 x 2 + x y ( x + 2 ) = 9
A. m ≥ 6
B. - 10 ≤ m ≤ 6
C. m ≤ - 10
D. m ≤ - 10 hoặc m ≥ 6
Tìm tất cả các giá trị thực của tham số m để hệ
3
2
x
+
x
+
1
-
3
2
+...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hệ 3 2 x + x + 1 - 3 2 + x + 1 + 2017 x ⩽ 2017 x 2 - ( m + 2 ) x + 2 m + 3 ⩾ 0 có nghiệm.
A. m ≤ - 2
B. m ⩾ - 3
C. m > - 3
D. m ≥ - 2
Tìm tất cả các giá trị thực của tham số m để hệ
3
2
x
+
x
+
1
-
3
2
+...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hệ 3 2 x + x + 1 - 3 2 + x + 1 + 2017 x ≤ 2017 x 2 - ( m + 2 ) x + 2 m + 3 ≥ 0 có nghiệm.
Tìm tất cả các giá trị của tham số m để hệ bất phương trình sau có nghiệm.
x
2
-
3
x
+
2
≤
0
m
x
2
-...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hệ bất phương trình sau có nghiệm.
x 2 - 3 x + 2 ≤ 0 m x 2 - 2 ( 2 m + 1 ) + 5 m + 3 ≥ 0
Ta có bất phương trình x 2 - 3x + 2 ≤ 0 ⇔ 1 ≤ x ≤ 2.
Yêu cầu bài toán tương đương với bất phương trình:
m x 2 – 2(2m + 1)x + 5m + 3 ≤ 0 (1) có nghiệm x ∈ S = [1;2].
Ta đi giải bài toán phủ định là: Tìm m để bất phương trình (1) vô nghiệm trên S
Tức là bất phương trình f(x) = m x 2 - 2(2m + 1)x + 5m + 3 < 0 (2) đúng với mọi x ∈ S.
• m = 0 ta có (2) -2x + 3 < 0 ⇔ x > 3/2 nên (2) không đúng với ∀x ∈ S
• m ≠ 0 tam thức f(x) có hệ số a = m, biệt thức Δ' = - m 2 + m + 1
Bảng xét dấu
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để hệ phương trình
x
2
-
m
y
(
x
+
m
y
)
x
2...
Đọc tiếp
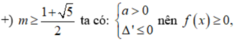
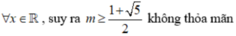
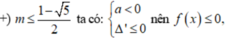
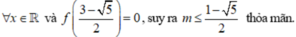
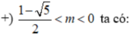
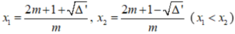
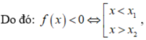
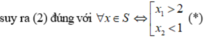
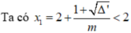
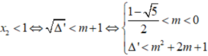
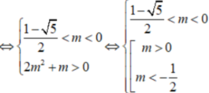
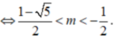
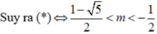
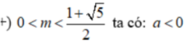
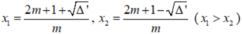
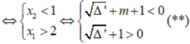
Tìm tất cả các giá trị của tham số m để hệ phương trình x 2 - m = y ( x + m y ) x 2 - y = x y có nghiệm
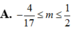
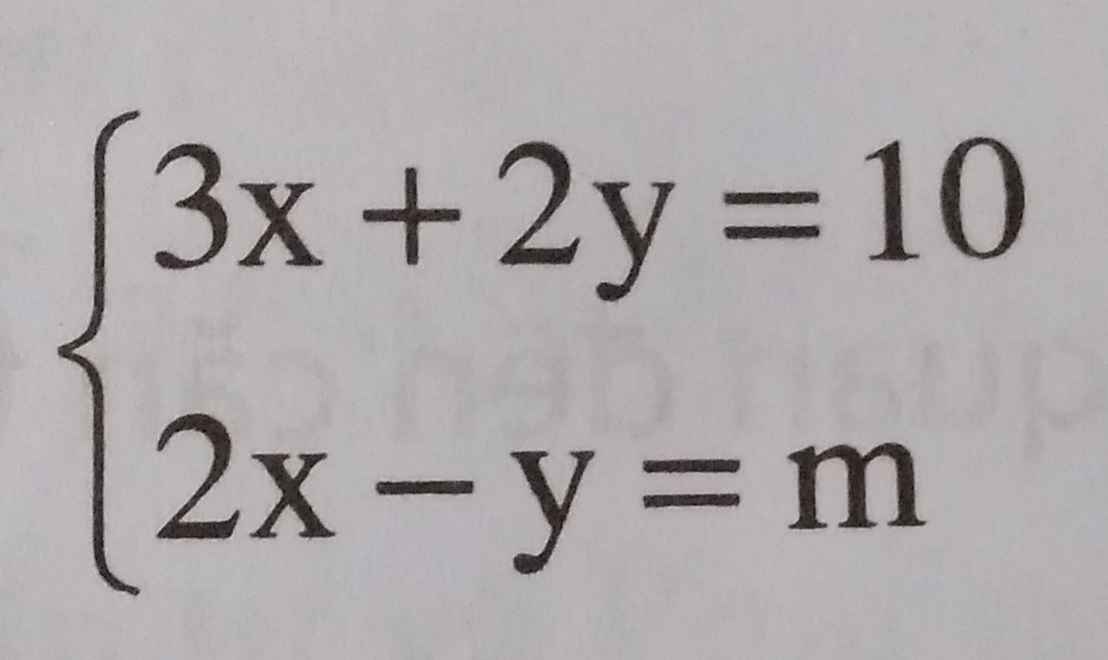
tìm tất cả các giá trị thực của tham số m để hệ phương trình có nghiệm (x;y) thỏa x>0, y<0.
\(\left\{{}\begin{matrix}3x+2y=10\\y=2x-m\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}3x+2(2x-m)=10\\y=2x-m\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}3x+4x-2m=10\\y=2x-m\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}7x=10+2m\\y=2x-m\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x=\dfrac{2m+10}{7}\\y=\dfrac{4m+20}{7}-m\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x=\dfrac{2m-10}{7}\\y=\dfrac{20-3m}{7}\end{matrix}\right.\)
Thay x và y vừa tìm dc vào điều kiện X>0 và Y<0
\(\dfrac{2m-10}{7}\)>0 => 2m-10>0 <=> m>5
\(\dfrac{20-3m}{7}\)<0 => 20-3m>0 <=> m<20/3
Vậy ...
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình
3
(
x
-
6
)
-
3
5
x
+...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình 3 ( x - 6 ) < - 3 5 x + m 2 > 7 có nghiệm.
A. m > -11.
B. m ≥ -11.
C. m < -11.
D. m ≤ -11.
Chọn A.
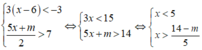
Hệ bất phương trình có nghiệm
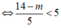⇔ 14 - m < 25 ⇔ -m < 11 ⇔ m > -11
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình
3
(
x
-
6
)
-
3
5
x
...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình
3 ( x - 6 ) < - 3 5 x + m 2 > 7 có nghiệm.
A. m > -11
B. m ≥ -11
C. m < -11
D. m ≤ -11
Chọn A
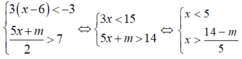
Hệ bất phương trình có nghiệm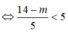 
hay 14 - m < 25 hay m > -11
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình
3
(
x
-
6
)
-
3
5
x
+...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình
3 ( x - 6 ) < - 3 5 x + m 2 > 7 có nghiệm.
A. m > -11
B. m ≥ -11
C. m < -11
D. m ≤ -11
Chọn A
Ta có:
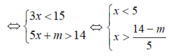
Hệ bất phương trình có nghiệm ⇔ 14 - m 5 < 5
Hay 14 - m < 25 tương đương m > -11
Đúng 0
Bình luận (0)