Question

Tìm tất cả các giá trị của tham số m để hệ bất phương trình sau có nghiệm.

x 2 - 3 x + 2 ≤ 0 m x 2 - 2 ( 2 m + 1 ) + 5 m + 3 ≥ 0

Answer 1

Ta có bất phương trình  x 2  - 3x + 2 ≤ 0 ⇔ 1 ≤ x ≤ 2.

Yêu cầu bài toán tương đương với bất phương trình:

m x 2  – 2(2m + 1)x + 5m + 3 ≤ 0 (1) có nghiệm x ∈ S = [1;2].

Ta đi giải bài toán phủ định là: Tìm m để bất phương trình (1) vô nghiệm trên S

Tức là bất phương trình f(x) = m x 2  - 2(2m + 1)x + 5m + 3 < 0 (2) đúng với mọi x ∈ S.

• m = 0 ta có (2) -2x + 3 < 0 ⇔ x > 3/2 nên (2) không đúng với ∀x ∈ S

• m ≠ 0 tam thức f(x) có hệ số a = m, biệt thức Δ' = - m 2  + m + 1

Bảng xét dấu
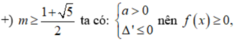
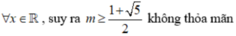
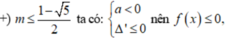
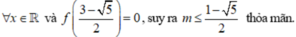
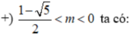
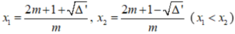
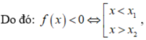
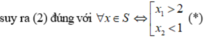
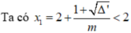
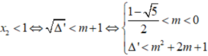
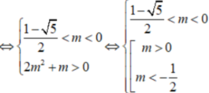
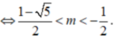
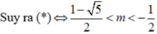
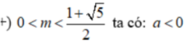
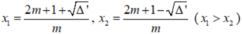
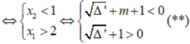