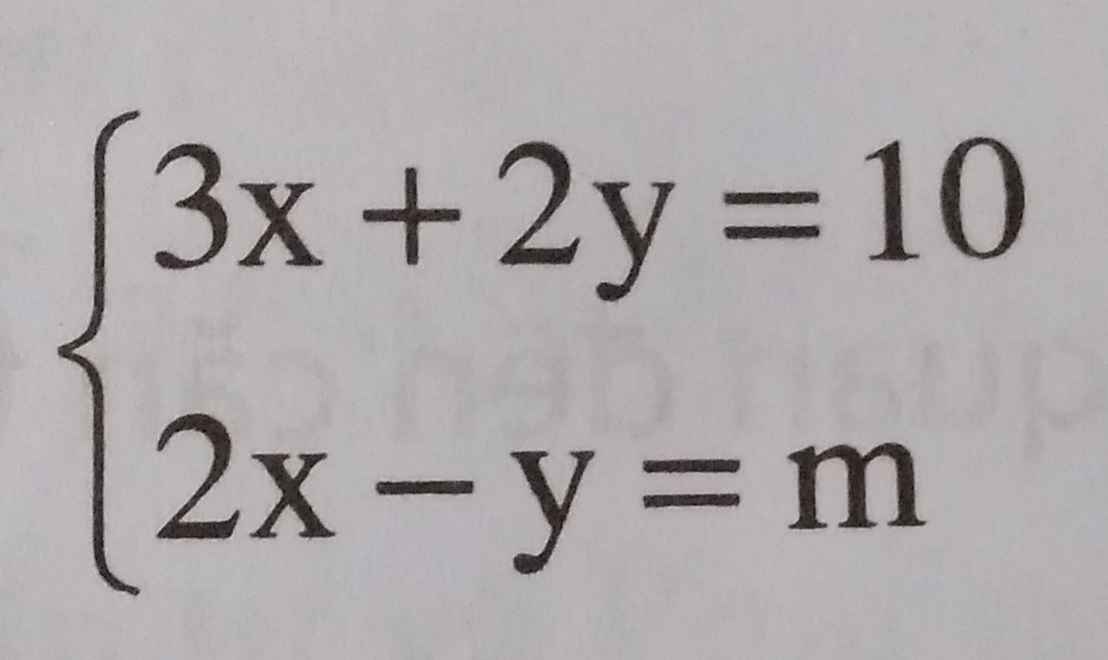\(\left\{{}\begin{matrix}3x+2y=10\\y=2x-m\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}3x+2(2x-m)=10\\y=2x-m\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}3x+4x-2m=10\\y=2x-m\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}7x=10+2m\\y=2x-m\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x=\dfrac{2m+10}{7}\\y=\dfrac{4m+20}{7}-m\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x=\dfrac{2m-10}{7}\\y=\dfrac{20-3m}{7}\end{matrix}\right.\)
Thay x và y vừa tìm dc vào điều kiện X>0 và Y<0
\(\dfrac{2m-10}{7}\)>0 => 2m-10>0 <=> m>5
\(\dfrac{20-3m}{7}\)<0 => 20-3m>0 <=> m<20/3
Vậy ...