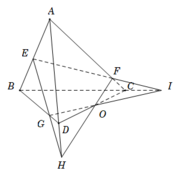
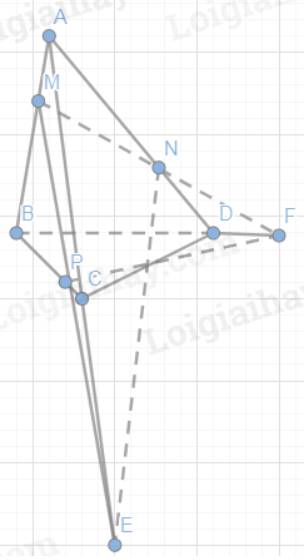
Cho tứ diện ABCD, các điểm E, F, G, H lần lượt thuộc các cạnh AD, AB, BC, CD sao cho
E A E D = F A F B = G C G B = H C H D
Khẳng định nào sau đây là đúng?
A. EFGH là hình bình hành.
B. EFGH có đúng một cặp cạnh song song.
C. EFGH là tứ giác không có cặt cạnh nào song song.
D. EFGH là hình chữ nhật.