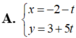
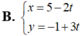
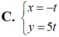
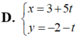
Phương trình tham số của đường thẳng qua M(1;-2) , N(4;3) là
\(\overrightarrow{MN}\left(3;5\right)\)
Vì (d) nhận vecto MN là vecto chỉ phương và đi qua điểm M(1;-2) nên phương trình tham số là:
\(\left\{{}\begin{matrix}x=1+3t\\y=-2+5t\end{matrix}\right.\)
cho tam giác ABC có A(-1;2), B(-2;-1) và C(3;-2)
a) Viết phương trình tham số của đường thẳng đi qua cạnh AC
b) Viết phương trình tham số của đường trung tuyến BN
c) Viết phương trình tham số của đường cao AH
d) Viết phương trình tham số của đường trung trực đoạn AB
e) Viết phương trình tham số của đường thẳng qua A và song song BC
f) Viết phương trình tham số của đường thẳng đi qua M(3;-1) và vuông góc với OB
g) Viết phương trình tham số của đường thẳng đi qua A và song song với
(d): \(\left\{{}\begin{matrix}x=2-5t\\y=1+2t\end{matrix}\right.\)
a: vecto AC=(4;-4)=(1;-1)
Phương trìh tham số là:
x=-1+t và y=2-t
b: Tọa độ N là:
\(\left\{{}\begin{matrix}x=\dfrac{-1+3}{2}=\dfrac{2}{2}=1\\y=\dfrac{2-2}{2}=0\end{matrix}\right.\)
N(1;0); B(-2;-1)
vecto BN=(3;1)
Phương trình tham số là:
x=1+3t và y=0+t=t
c: vecto BC=(5;-1)
=>vecto AH=(1;5)
Phương trình tham số AH là:
x=-1+t và y=2+5t
Cho đường thẳng ∆ đi qua điểm M(2;0;-1) và có vectơ chỉ phương a → = ( 4 ; - 6 ; 2 ) . Phương trình tham số của đường thẳng ∆ là:
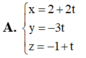
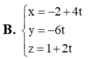
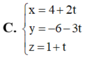
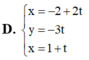
Phương trình tham số của đường thẳng d qua điểm M( -2 ; 3) và vuông góc với đường thẳng d’ : 3x - 4y +1= 0 là:
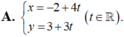
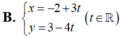
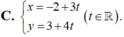
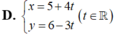
Do 2 đường thẳng d và d’ vuông góc với nhau nên d có véc tơ chỉ phương
.
Mà d đi qua điểm M( -2; 3) nên d có phương trình tham số là:
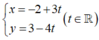
Chọn B.
trong mặt phẳng oxy, viết phương trình tham số của đường thẳng qua M(1;-2), N(4;3)
\(\left\{{}\begin{matrix}VTCP\left(3;5\right)\\M\left(1;-2\right)\end{matrix}\right.\)
VTTS \(\left\{{}\begin{matrix}x=1+3t\\y=-2+5t\end{matrix}\right.\)
Lập phương trình tham số của đường thẳng: Đi qua M(2 ; 3 ; -5) và song song với đường thẳng (Δ): ∆ : x = - 2 + 2 t y = 3 - 4 t z = - 5 t
(Δ) nhận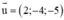 
là 1 vtcp
+ (d) cần tìm song song với (Δ)
⇒ (d) nhận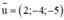 
là 1 vtcp
+ (d) đi qua M(2; 3; -5)
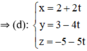
Phương trình tham số của đường thẳng (d) đi qua điểm M( 2; -5) và vuông góc với đường thẳng (d’) : x+ 6y -7= 0 là:
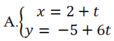
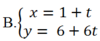
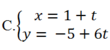
D.Tất cả sai
Đáp án A
Do 2 đường thẳng d và (d’) vuông góc với nhau nên VTCP của đường thẳng này là VTPT của đường thẳng kia và ngược lại.
Mà đường thẳng (d’) có VTPT là n → ( 1 ; 6 ) n ê n u → ( 1 ; 6 ) là VTCP của đường thẳng (d) .
Khi đó phương trình tham số của đường thẳng (d) cần tìm là:
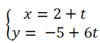
Phương trình tham số của đường thẳng ∆ đi qua điểm M(2; 3) và có hệ số góc k = 4 là:
A.y = 4(x – 2) + 3
B. 4x – y – 5 = 0
C. x = 2 + t y = 3 + 4 t , t ∈ R
D. x = 2 + 2 t y = 3 + t , t ∈ R
Hướng dẫn:
Đường thẳng ∆ có hệ số góc k = 4 nên có vectơ chỉ phương u → = 1 ; 4 . Do đó C là phương án đúng.
Chú ý. Học sinh có thể nhầm sang các loại phương trình khác của đường thẳng như các phương án ở A và B. Đây đều là phương trình của đường thẳng nhưng không là phương trình tham số.
