Với n là số nguyên dương, gọi a 3 n − 3 là hệ số của x 3 n − 3 trong khai triển thành đa thức của x 2 + 1 n x + 2 n . Tìm n để a 3 n − 3 = 26 n .
A. n = 7
B. n = 5
C. n = 6
D. n = 4
Với n là số nguyên dương, gọi a 3 n - 3 là hệ số của x 3 n - 3 trong khai triển thành đa thức của x 2 + 1 n x + 2 n . Tìm n để a 3 n - 3 = 26 n
A: 5
B: 6
C: 7
D: 8
Ta có : 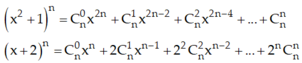
Dễ dàng kiểm tra n=1; n=2 không thoả mãn điều kiện bài toán.
Với n ≥ 3 thì dựa vào khai triển ta chỉ có thể phân tích
![]()
Do đó hệ số của x3n-3 trong khai triển thành đa thức của
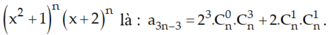
Suy ra  hoặc n = 5
hoặc n = 5
Vậy n=5 là giá trị cần tìm.
Chọn A.
Gọi a 2018 là hệ số của số hạng chứa x 2018 trong khai triển nhị thức Niutơn x − x n với x ≥ 0 ; n là số nguyên dương thỏa mãn 1 2 ! .2017 ! + 1 4 ! .2015 ! + 1 6 ! .2013 ! ... + 1 2016 ! .3 ! + 1 2018 ! = 2 2018 − 1 P n . Tìm a 2018
A. 2017
B. − C 2018 3 .
C. 2019
D. C 2019 2 .
Gọi S(n) là tổng tất cả các chữ số của số nguyên dương n khi biểu diễn nó trong hệ thập phân. Biết rằng với mọi số nguyên dương n thì ta có 0<S(n)<=n. Tìm số nguyên dương n sao cho S(n)=n^2- 2011n+ 2010
\(^∗\)Xét \(n=2011\)thì \(S\left(2011\right)=2011^2-2011.2011+2010=2010\)(vô lí)
\(^∗\)Xét \(n>2011\)thì \(n-2011>0\)do đó \(S\left(n\right)=n\left(n-2011\right)+2010>n\left(n-2011\right)>n\)(vô lí do \(S\left(n\right)\le n\))
* Xét \(1\le n\le2010\)thì \(\left(n-1\right)\left(n-2010\right)\le0\Leftrightarrow n^2-2011n+2010\le0\)hay \(S\left(n\right)\le0\)(vô lí do \(S\left(n\right)>0\))
Vậy không tồn tại số nguyên dương n thỏa mãn đề bài
Tìm hệ số của số hạng chứa x 8 trong khai triển nhị thức Newton của 1 x 3 + x 5 n , biết rằng C n + 4 n + 1 - C n + 3 n = 7 ( n + 3 ) . (với n là số nguyên dương và x > 0)
A. 400
B. 480
C. 495
D. 0
Gọi n là số nguyên dương sao cho 1 log 3 x × 1 log 3 3 x + 1 log 3 2 x + . . . . . + 1 log 3 n x = 190 log 3 x đúng với mọi x dương, x ≠ 1 . Tìm giá trị của biểu thức P = 2 n + 3
A. P = 23.
B. P = 41.
C. P = 43.
D. P = 32.
Gọi n là số nguyên dương sao cho 1 log 3 x + 1 log 3 2 x + 1 log 3 3 x + ... + 1 log 3 n x = 210 log 3 x đúng với mọi x dương. Tìm giá trị của biểu thức P = 2 n + 3 .
A. P = 32 .
B. P = 40 .
C. P = 43 .
Đáp án C
Ta có: 1 log 3 x + 2 log 3 x + 3 log 3 x + ... + n log 3 x = 210 log 3 x
n n + 1 2 log 3 x = 210 log 3 x ⇔ n n + 1 = 420 ⇔ n = 20 ⇒ P = 2.20 + 3 = 43
Gọi n là số nguyên dương sao cho 1 log 3 x + 1 log 3 2 x + 1 log 3 3 x + . . . + 1 log 3 n x = 210 log 3 x đúng với mọi x dương. Tìm giá trị của biểu thức P = 2n + 3.
A. P = 32
B. P = 40
C. P = 43
D. P = 23
Đáp án C
Ta có:
1 log 3 x + 1 log 3 2 x + 1 log 3 3 x + . . . + 1 log 3 n x = 210 log 3 x
⇔ n n + 1 2 log 3 x = 210 log 3 x
<=> n(n+1) = 420
<=> n = 20
=> P = 2.20+3 = 43.
Gọi n là số nguyên dương sao cho 1 log 3 x + 1 log 3 2 x + 1 log 3 3 x + . . . + 1 log 3 n x = 210 log 3 x đúng với mọi x dương. Tìm giá trị của biểu thức P = 2n + 3.
A. P = 32
B. P = 40
C. P = 43
D. P = 23
Đáp án C
Ta có: 1 log 3 x + 2 log 3 x + 3 log 3 x + . . . + n log 3 x = 210 log 3 x
⇔ n n + 1 2 log 3 x = 210 log 3 x ⇔ n n + 1 = 420 ⇔ n = 20 ⇒ P = 2 . 20 + 3 = 43 .
cho 3 số nguyên x y z . Gọi a là tích của x y z . lập câu lệnh viết a thành một lũy thứa bậc n của một số nguyên dương thì số mũ lớn nhất là bao nhiêu trong python