Cho hàm số y = 4 x + 2 cos 2 x có đồ thị là (C). Hoành độ của các điểm trên (C) mà tại đó tiếp tuyến của (C) song song hoặc trùng với trục hoành là
A. x = π 4 + k π k ∈ ℤ .
B. x = π 2 + k π k ∈ ℤ .
C. x = π + k π k ∈ ℤ .
D. x = k 2 π k ∈ ℤ .
Những câu hỏi liên quan
Cho hàm số y x3 – 2x2 + 2x có đồ thị (C). Gọi x1, x2 là hoành độ các điểm M, N trên (C), mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y -x + 2017. Khi đó x1 + x2 bằng: A. 4/3. B. -4/3. C. 1/3. D. -1.
Đọc tiếp
Cho hàm số y = x3 – 2x2 + 2x có đồ thị (C). Gọi x1, x2 là hoành độ các điểm M, N trên (C), mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y = -x + 2017. Khi đó x1 + x2 bằng:
A. 4/3.
B. -4/3.
C. 1/3.
D. -1.
Chọn A.
Ta có: y’ = 3x2 – 4x + 2.
Tiếp tuyến tại M, N của (C) vuông góc với đường thẳng y = -x + 2017. Nên tiếp tuyến tại M và N có hệ số góc là 1
Hoành độ x1, x2 của các điểm M, N là nghiệm của phương trình 3x2 – 4x + 2 = 1.
Suy ra x1 + x2 = 4/3 ( hệ thức Vi-et).
Đúng 0
Bình luận (0)
a) tìm hệ số góc của tiếp tuyến của đồ thị hàm số y=-x^3+3x-2 (c) tại điểm có hoành độ -3
b) viết phương trình tiếp tuyến của đồ thị hàm số (c) trên tại điểm ( ứng với tiếp điểm ) có hoành độ -3
1)Viết phương trình tiếp tuyến của đường cong (C):yf(x)x^3-2x biết: a)tiếp tuyến vuông góc với trục Ox. b)Tại giao điểm của (C) với các trục tọa độ.2)Cho hàm số :yf(x)x-1/x có đồ thị là đường cong (C):a) Viết pt tt với (C),biết tt song song với dt y2x và tiếp điểm có hoành độ âm.b)CMR trên (C) không thể tồn tại 2 điểm M,N để tiếp tuyến tại 2 điểm này vuông góc với nhau.c)CMR mọi tiếp tuyến của (C) đều không thể đi qua gốc tọa độ O.3)Tìm tất cả các điểm trên đồ thị (C):yf(x)(2x+3)/(x+2) sao cho t...
Đọc tiếp
1)Viết phương trình tiếp tuyến của đường cong (C):y=f(x)=x^3-2x biết: a)tiếp tuyến vuông góc với trục Ox. b)Tại giao điểm của (C) với các trục tọa độ.
2)Cho hàm số :y=f(x)=x-1/x có đồ thị là đường cong (C):
a) Viết pt tt với (C),biết tt song song với dt y=2x và tiếp điểm có hoành độ âm.
b)CMR trên (C) không thể tồn tại 2 điểm M,N để tiếp tuyến tại 2 điểm này vuông góc với nhau.
c)CMR mọi tiếp tuyến của (C) đều không thể đi qua gốc tọa độ O.
3)Tìm tất cả các điểm trên đồ thị (C):y=f(x)=(2x+3)/(x+2) sao cho tại điểm đó tt của (C) cắt các đường thằng (d1):x=-2 và (d2):y=2 lần lượt tại A và B sao cho AB gần nhất.
4)Cho hàm số y=f(x)=sin2x+1 (x>=0) và =2x+1 (x<0) .Tính đạo hàm của hàm số tại Xo=0 bằng định nghĩa.
Cho hàm số y f(x) có đạo hàm trên R và đồ thị (C). Tiếp tuyến của đồ thị (C) tại điểm (2;m) có phương trình là
y
4
x
-
6
. Tiếp tuyến của các đồ thị hàm số
y
f
f
x
và
y
f
3
x
2
-
10...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm trên R và đồ thị (C). Tiếp tuyến của đồ thị (C) tại điểm (2;m) có phương trình là y = 4 x - 6 . Tiếp tuyến của các đồ thị hàm số y = f f x và y = f 3 x 2 - 10 tại điểm có hoành độ bằng 2 có phương trình lần lượt là y = a x + b v à y = c x + d . Tính giá trị của biểu thức S = 4 a + 3 c - 2 b + d
A. S = -26
B. S = 176
C. S = 178
D. S = 174
Cho đồ thị hàm số
y
x
3
-
2
x
2
+
2
x
(C). Gọi
x
1
,
x
2
là hoành độ các điểm M, N trên (C), mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng
y
-
x
+
2017
. Khi đó
x
1
,...
Đọc tiếp
Cho đồ thị hàm số y = x 3 - 2 x 2 + 2 x (C). Gọi x 1 , x 2 là hoành độ các điểm M, N trên (C), mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y = - x + 2017 . Khi đó x 1 , x 2 bằng
A. 4
B. - 4 3
C. 4 3
D. -1
Tiếp tuyến của C vuông góc với đường thẳng y= -x + 2017 nên hệ số góc của tiếp tuyến là k 2 thỏa mãn ( - 1 ) k 2 = - 1 ⇒ k 2 = 1
Suy ra k 2 = y ' = 1 ⇒ 3 x 2 - 4 x + 2 ⇔ 3 x 2 - 4 x + 2 = 0 ( * )
Vì x 1 , x 2 là nghiệm của (*) nên áp dụng Vi-ét ta có x 1 + x 2 = 4 3
Chọn C
Đúng 0
Bình luận (0)
Cho hàm số
y
cos
2
x
.a) Chứng minh rằng cos
2
x
+
k
π
cos
2
x
với mọi số nguyên k. Từ đó vẽ đồ thị (C) của hàm số
y
cos
2
x
.b) Viết phương...
Đọc tiếp
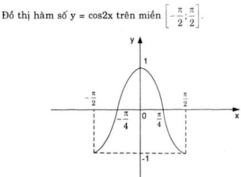
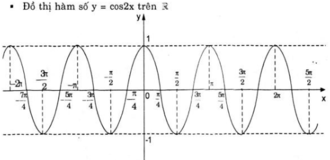
Cho hàm số y = cos 2 x .
a) Chứng minh rằng cos 2 x + k π = cos 2 x với mọi số nguyên k. Từ đó vẽ đồ thị (C) của hàm số y = cos 2 x .
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π / 3 .
c) Tìm tập xác định của hàm số : z = 1 - cos 2 x 1 + cos 2 2 x
a) + Hàm số y = cos x có chu kì 2π.
Do đó: cos 2.(x + kπ) = cos (2x + k2π) = cos 2x.
⇒ Hàm số y = cos 2x cũng tuần hoàn với chu kì π.
Từ đó suy ra
b. y = f(x) = cos 2x
⇒ y’ = f’(x) = (cos 2x)’ = -(2x)’.sin 2x = -2.sin 2x.
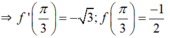
⇒ Phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π/3 là:
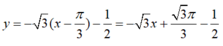
c. Ta có: 1 – cos 2x = 2.sin2x ≥ 0.
Và 1 + cos22x > 0; ∀ x
⇒ 
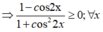
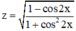luôn xác định với mọi x ∈ R.
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
−
2
x
2
+
2
x
có đồ thị (C). Gọi
x
1
,
x
2
là hoành độ các điểm M, N trên (C) mà tại đó tiếp tuyến với (C) vuông góc với đường thẳng
y
−
x
+
2018
. Khi đó
x
1...
Đọc tiếp
Cho hàm số y = x 3 − 2 x 2 + 2 x có đồ thị (C). Gọi x 1 , x 2 là hoành độ các điểm M, N trên (C) mà tại đó tiếp tuyến với (C) vuông góc với đường thẳng y = − x + 2018 . Khi đó x 1 + x 2 bằng:
A. 8 3 .
B. 2 3 .
C. 4 3 .
D. 5 3 .
Đáp án C
y ' = 3 x 2 − 4 x + 2
Do tại các điểm M, N tiếp tuyến với vuông góc với đường thẳng y = − x + 2018
nên
3 x 2 − 4 x + 2 . − 1 = − 1 ⇔ 3 x 2 − 4 x + 1 = 0 ⇔ x = 1 x = 1 3
Suy ra x 1 + x 2 = 1 + 1 3 = 4 3 .
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
−
2
x
2
+
2
x
có đồ thị (C). Gọi
x
1
,
x
2
là hoành độ các điểm M, N trên (C) mà tại đó tiếp tuyến với (C) vuông góc với đường thẳng
y
−
x
+
2018
. Khi đó
x
1...
Đọc tiếp
Cho hàm số y = x 3 − 2 x 2 + 2 x có đồ thị (C). Gọi x 1 , x 2 là hoành độ các điểm M, N trên (C) mà tại đó tiếp tuyến với (C) vuông góc với đường thẳng y = − x + 2018 . Khi đó x 1 + x 2 bằng
A. 8 3 .
B. 2 3 .
C. 4 3 .
D. 5 3 .
Cho hàm số y = x 4 + x 2 − 3 có đồ thị (C). Khi đó hệ số góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = 1 là
A. -1
B. 2
C. -4
D. 6
