Trong không gian cho hình thoi ABCD có cạnh là 5cm và góc A B C ⏜ = 60 ° . Tính diện tích xung quanh S của hình thu được khi quay hình thoi quanh trục DB.
A. S = 25 π 3 3 c m 2
B. S = 25 π c m 2
C. S = 25 π 3 4 c m 2
D. S = 25 π 3 cm 2
Những câu hỏi liên quan
Trong không gian cho hình thoi ABCD có cạnh là 5cm và góc
A
B
C
^
60
°
. Tính diện tích xung quanh S của hình thu được khi quay hình thoi quanh trục DB. A.
S
25
π
3
3
c
m
2
B.
S
25...
Đọc tiếp
Trong không gian cho hình thoi ABCD có cạnh là 5cm và góc A B C ^ = 60 ° . Tính diện tích xung quanh S của hình thu được khi quay hình thoi quanh trục DB.
A. S = 25 π 3 3 c m 2
B. S = 25 π c m 2
C. S = 25 π 3 4 c m 2
D. S = 25 π 3 c m 2
Trong không gian cho hình thoi ABCD có cạnh là 5cm và góc
A
B
C
^
60
0
. Tính diện tích xung quanh S của hình thu được khi quay hình thoi quanh trục DB.
A
.
S
25
π
3
3
...
Đọc tiếp
Trong không gian cho hình thoi ABCD có cạnh là 5cm và góc A B C ^ = 60 0 . Tính diện tích xung quanh S của hình thu được khi quay hình thoi quanh trục DB.
A . S = 25 π 3 3 c m 2
B . S = 25 π c m 2
C . S = 25 π 3 4 c m 2
D . S = 25 π 3 c m 2
Đáp án B.
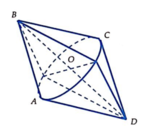
Do 
=> AC= 5cm
Do đó diện tích của hình thu được:
Đúng 0
Bình luận (0)
Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60°. Tính diện tích xung quanh và thể tích của hình nón có đỉnh S và đáy là đường tròn ngoại tiếp đáy hình chóp S.ABCD. Khi đó diện tích xung quanh và thể tích của hình nón bằng A.
S
xq
πa
2
;
V
πa
3...
Đọc tiếp
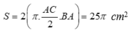
Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60°. Tính diện tích xung quanh và thể tích của hình nón có đỉnh S và đáy là đường tròn ngoại tiếp đáy hình chóp S.ABCD. Khi đó diện tích xung quanh và thể tích của hình nón bằng
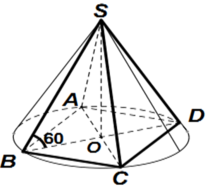
A. S xq = πa 2 ; V = πa 3 6 12
B. S xq = πa 2 ; V = πa 3 3 12
C. S xq = 2 πa 2 ; V = πa 3 3 12
D. S xq = 2 πa 2 ; V = πa 3 6 6
Đáp án A
Gọi O là tâm của hình vuông ABCD.
Do S.ABCD là hình chóp đều nên SO ⊥ (ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)
Đúng 0
Bình luận (0)
Cho lăng trụ đứng
A
B
C
D
.
A
B
C
D
có đáy ABCD là hình thoi có độ dài cạnh 3cm, góc
∠
A
B
C
60
o
và chiều cao AA’ của hình lăng trụ bằng 4cm. Tính:a) Diện tích xung quanh của hình lăng trụ.b) Thể tích của hình lăng trụ đó.
Đọc tiếp
Cho lăng trụ đứng A B C D . A ' B ' C ' D ' có đáy ABCD là hình thoi có độ dài cạnh 3cm, góc ∠ A B C = 60 o và chiều cao AA’ của hình lăng trụ bằng 4cm. Tính:
a) Diện tích xung quanh của hình lăng trụ.
b) Thể tích của hình lăng trụ đó.
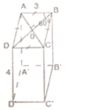
a) Sxq = 2.P.H (p: chu vi đáy; h: chiều cao)
= 3(3 + 3).4 = 48(cm2)
b) Gọi O là giao điểm của AC và BD. Vì tứ giác ABCD là hình thoi nên AC ⊥ BD tại O và có ∠ABC = 60o => ∠ABO = 30o
ΔABO là nửa tam giác đều nên
Đúng 0
Bình luận (0)
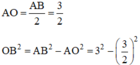
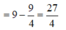
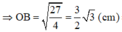
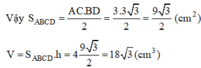
Cho hình chóp tứ giác đều S.ABCD, đáy ABCD là hình vuông có cạnh 3cm, cạnh bên SA = 5cm.
a) Tính đường cao SH của hình chóp.
b) Tính diện tích xung quanh và thể tích của hình chóp.
a) Ta có: AC2 = AB2 + BC2 (Pytago) = 32 + 32 = 18(cm)
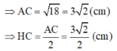
Lại có: SH2 = SC2 - HC2 (Pytago)
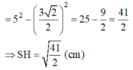
b) Gọi K là trung điểm của BC
Ta có: SK2 = SH2 + HK2 (Pytago)
Đúng 0
Bình luận (0)
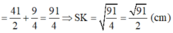
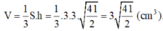
a) Ta có: AC2 = AB2 + BC2 (Pytago) = 32 + 32 = 18(cm)
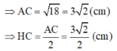
Lại có: SH2 = SC2 - HC2 (Pytago)
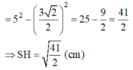
b) Gọi K là trung điểm của BC
Ta có: SK2 = SH2 + HK2 (Pytago)
Đúng 0
Bình luận (0)
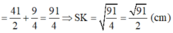
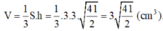
Bài: cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Tính thể tích và diện tích xung quanh của chóp, biết:
a. Góc trong SB và đáy bằng 45°
b. Góc trong (SCD) và đáy bằng 60°
Đề bài thiếu 1 dữ liệu nữa (ví dụ SA vuông góc mặt đáy)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy. Tính thể tích và diện tích xung quanh của chóp, biết:
a. Góc trong SB và đáy bằng 45°
b. Góc trong (SCD) và đáy bằng 60°
a.
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SBA}\) là góc giữa SB và đáy
\(\Rightarrow\widehat{SBA}=45^0\Rightarrow SA=AB.tan45^0=a\)
\(V=\dfrac{1}{3}SA.AB^2=\dfrac{a^3}{3}\)
\(SB=SD=\sqrt{SA^2+AB^2}=a\sqrt{2}\)
\(S_{xq}=\dfrac{1}{2}SA.AD+\dfrac{1}{2}SA.AB+\dfrac{1}{2}SB.BC+\dfrac{1}{2}SD.CD=a^2\left(\sqrt{2}+1\right)\)
b.
\(CD\perp\left(SAD\right)\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và đáy
\(\Rightarrow\widehat{SDA}=60^0\)
\(\Rightarrow SA=AD.tan60^0=a\sqrt{3}\)
\(V=\dfrac{1}{3}SA.AB^2=\dfrac{a^3\sqrt{3}}{3}\)
\(SB=SD=\sqrt{SA^2+AD^2}=2a\)
\(S_{xq}=\dfrac{1}{2}SA.AB+\dfrac{1}{2}SA.AD+\dfrac{1}{2}SB.BC+\dfrac{1}{2}SD.CD=3a^2\)
Đúng 1
Bình luận (0)
cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy là hình thoi. AB=8cm, \(\widehat{BAD}=\widehat{ACA'=60}\) BAD= góc ACA'=60 độ. tính diện tích xung quanh và diện tích toàn phần của hình lăng trụ
Cho hình lăng trụ đứng ABCD.ABCD’ có đáy là hình thoi cạnh 3 cm,
A
B
C
^
60
°
và chiều cao bằng 5 cm.a) Tính diện tích xung quanh lăng trụ.b) Tính diện tích toàn phần lăng trụ.c) Tính thể tích lăng trụ.
Đọc tiếp
Cho hình lăng trụ đứng ABCD.A'B'C'D’ có đáy là hình thoi cạnh 3 cm, A B C ^ = 60 ° và chiều cao bằng 5 cm.
a) Tính diện tích xung quanh lăng trụ.
b) Tính diện tích toàn phần lăng trụ.
c) Tính thể tích lăng trụ.
