a.
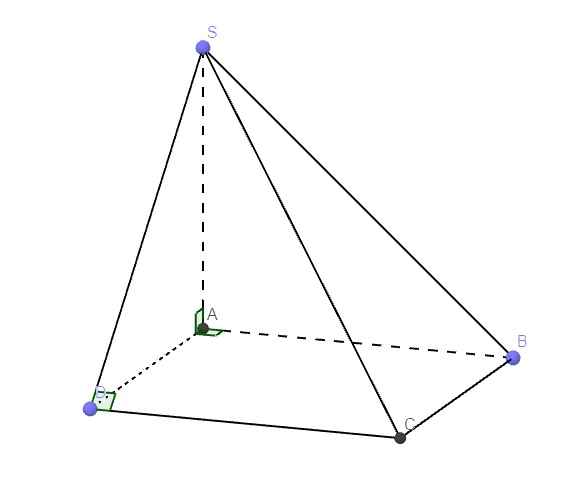
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SBA}\) là góc giữa SB và đáy
\(\Rightarrow\widehat{SBA}=45^0\Rightarrow SA=AB.tan45^0=a\)
\(V=\dfrac{1}{3}SA.AB^2=\dfrac{a^3}{3}\)
\(SB=SD=\sqrt{SA^2+AB^2}=a\sqrt{2}\)
\(S_{xq}=\dfrac{1}{2}SA.AD+\dfrac{1}{2}SA.AB+\dfrac{1}{2}SB.BC+\dfrac{1}{2}SD.CD=a^2\left(\sqrt{2}+1\right)\)
b.
\(CD\perp\left(SAD\right)\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và đáy
\(\Rightarrow\widehat{SDA}=60^0\)
\(\Rightarrow SA=AD.tan60^0=a\sqrt{3}\)
\(V=\dfrac{1}{3}SA.AB^2=\dfrac{a^3\sqrt{3}}{3}\)
\(SB=SD=\sqrt{SA^2+AD^2}=2a\)
\(S_{xq}=\dfrac{1}{2}SA.AB+\dfrac{1}{2}SA.AD+\dfrac{1}{2}SB.BC+\dfrac{1}{2}SD.CD=3a^2\)