Cho hàm số f(x) có f ( 1 ) = 1, f ( m + n ) = f ( m ) + f ( n ) + m n , ∀ m , n ∈ ℕ * . Giá trị của biểu thức T = log f ( 96 ) − f ( 69 ) − 241 2 là
A.4
B.3
C.6
D.9
Cho hàm số f(x) có f ( 1 ) = 1 , f ( m + n ) = f ( m ) + f ( n ) + m n , ∀ m , n ∈ ℕ * . Giá trị của biểu thức T = log f ( 96 ) − f ( 69 ) − 241 2 là
A. 4
B. 3
C. 6
D. 9
Cho hàm số f ( x ) = 1 2 log 2 ( 2 x 1 - x ) và hai số thực m, n thuộc khoảng (0; 1) sao cho m +n = 1. Tính f(m) + f(n).
A. 2
B. 0
C. 1
D. 1 2
cho hàm số f(x) xác định trên tập N biết f(2)=0, f(3)>0, f(2001)=667 và f(m)+f(n)<=f(m+n)<=f(m)+f(n)+1
Cho hàm số f ( x ) = 1 2 log 2 2 x 1 - x và hai số thực m, n thuộc khoảng (0;1) sao cho m + n = 1 . Tính f ( m ) + f ( n )
A. 2
B. 0
C. 1
D. 1 2
Cho hàm số f(x) có đồ thị của hàm số f'(x) như hình vẽ. Biết f(0) + f(1) - 2f(2) = f(4) - f(3). Giá trị nhỏ nhất m, giá trị lớn nhất M của hàm số f(x) trên đoạn [0;4] là
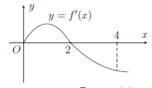
A. m = f(4), M = f(1)
B. m = f(4), M = f(2)
C. m = f(1), M = f(2)
D. m = f(0), M = f(2)
Chọn B
Từ đồ thị của hàm số f'(x) trên đoạn [0;4] ta có bảng biến thiên của hàm số trên đoạn [0;4] như sau:
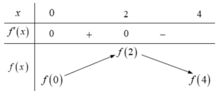
Từ bảng biến thiên ta có ![]()
Mặt khác ![]()
![]()
![]()
![]()
Suy ra ![]()
Cho hàm số f(x) có đạo hàm là hàm f'(x). Đồ thị hàm số f'(x) như hình vẽ bên. Biết rằng f(0) + f(1) - 2f(2) = f(4) - f(3). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4].

A. m = f(4), M = f(2)
B. m = f(1), M = f(2)
C. m = f(4), M = f(1)
D. m = f(0), M = f(2)
Chọn A
Dựa vào đồ thị của hàm f'(x) ta có bảng biến thiên.
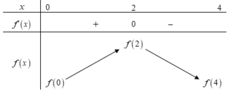
Vậy giá trị lớn nhất M = f(2)
Hàm số đồng biến trên khoảng (0;2) nên f(2) > f(1) => f(2) - f(1) > 0 .
Hàm số nghịch biến trên khoảng (2;4) nên f(2) > f(3) => f(2) - f(3) > 0.
Theo giả thuyết: f(0) + f(1) - 2f(2) = f(4) - f(3).
![]()
=> f(0) > f(4)
Vậy giá trị nhỏ nhất m = f(4)
Cho hàm số y=f(x)=(m-2)x có đồ thị đi qua điểm A(10;-15)
a) Tìm m
b) Vẽ đồ thị hàm số
c) Tính f(-2); f(-1); f(0); f(1/2)
d) Chứng tỏ rằng: f(-4)-f(-6)=f(2)
a: Thay x=10 và y=-15 vào f(x), ta được:
10m-20=-15
=>10m=5
hay m=1/2
hàm số f(x)cho bởi công thức ;f(x)=x^2-x+1.CMR với mọi m thuộc N,m>1 thì m,f(m),f(f(m))nguyên tố cùng nhau từng đôi một
Cho hàm số f ( x ) = e 1 + 1 x 2 + 1 ( x + 1 ) 2 , biết rằng f ( 1 ) . f ( 2 ) . f ( 3 ) . . . f ( 2017 ) = e m n với m, n là các số tự nhiên và m 2 tối giản. Tính m - n 2
A. m - n 2 = 2018
B. m - n 2 = 1
C. m - n 2 = -2018
D. m - n 2 = -1