Các câu hỏi tương tự
Cho f(1) 1; f(m + n) f(m) + f( n) + m.n với các số nguyên dương m; n .Khi đó giá trị của biểu thức
T
log
f
2017
-
f
2016
-
17
2
là A. 3 B. 4 C. 6 D. 9
Đọc tiếp
Cho f(1) = 1; f(m + n) = f(m) + f( n) + m.n với các số nguyên dương m; n .Khi đó giá trị của biểu thức T = log f 2017 - f 2016 - 17 2 là
A. 3
B. 4
C. 6
D. 9
Cho hàm số f(x) có đồ thị của hàm số f(x) như hình vẽ. Biết f(0) + f(1) - 2f(2) f(4) - f(3). Giá trị nhỏ nhất m, giá trị lớn nhất M của hàm số f(x) trên đoạn [0;4] là A. m f(4), M f(1) B. m f(4), M f(2) C. m f(1), M f(2) D. m f(0), M f(2)
Đọc tiếp
Cho hàm số f(x) có đồ thị của hàm số f'(x) như hình vẽ. Biết f(0) + f(1) - 2f(2) = f(4) - f(3). Giá trị nhỏ nhất m, giá trị lớn nhất M của hàm số f(x) trên đoạn [0;4] là
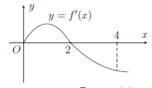
A. m = f(4), M = f(1)
B. m = f(4), M = f(2)
C. m = f(1), M = f(2)
D. m = f(0), M = f(2)
Cho hàm số f(x) có đạo hàm là hàm f(x). Đồ thị hàm số f(x) như hình vẽ bên. Biết rằng f(0) + f(1) - 2f(2) f(4) - f(3). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4]. A. m f(4), M f(2) B. m f(1), M f(2) C. m f(4), M f(1) D. m f(0), M f(2)
Đọc tiếp
Cho hàm số f(x) có đạo hàm là hàm f'(x). Đồ thị hàm số f'(x) như hình vẽ bên. Biết rằng f(0) + f(1) - 2f(2) = f(4) - f(3). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4].

A. m = f(4), M = f(2)
B. m = f(1), M = f(2)
C. m = f(4), M = f(1)
D. m = f(0), M = f(2)
Cho a, b, c, d, e, f là các số thực thỏa mãn
(
d
-
1
)
2
+
e
-
2
2...
Đọc tiếp
Cho a, b, c, d, e, f là các số thực thỏa mãn
( d - 1 ) 2 + e - 2 2 + f - 3 2 = 1 a + 3 2 + b - 2 2 + c 2 = 9
Gọi giá trị lớn nhất, giá trị nhỏ nhất của biểu thức F = a - d 2 + b - e 2 + c - f 2 lần lượt là M, m
Khi đó, M - m bằng:
A. 10
B. 10
C. 8
D. 2 2
Cho hàm số yf(x),
x
∈
-
2
;
3
có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn
-
2
;
3
. Giá trị của M+n là A. 6 B. 1 C. 5 D. 3
Đọc tiếp
Cho hàm số y=f(x), x ∈ - 2 ; 3 có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn - 2 ; 3 . Giá trị của M+n là
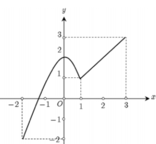
A. 6
B. 1
C. 5
D. 3
Cho hàm số
f
(
x
)
e
1
+
1
x
2
+
1
(
x
+...
Đọc tiếp
Cho hàm số f ( x ) = e 1 + 1 x 2 + 1 ( x + 1 ) 2 , biết rằng f ( 1 ) . f ( 2 ) . f ( 3 ) . . . f ( 2017 ) = e m n với m, n là các số tự nhiên và m 2 tối giản. Tính m - n 2
A. m - n 2 = 2018
B. m - n 2 = 1
C. m - n 2 = -2018
D. m - n 2 = -1
Cho hàm số
f
(
x
)
x
3
+
8
x
+
m...
Đọc tiếp
Cho hàm số f ( x ) = x 3 + 8 x + m x - 1 k h i x ≠ 1 n k h i x = 1 , với m,n là các tham số thực. Biết rằng hàm số f(x) liên tục tại x=1 , khi đó tổng giá trị m+n bằng:
A. 4.
B. 1.
C. 0.
D. 2.
Cho hàm số f(x) xác định trên
ℝ
-
2
;
1
thỏa mãn
f
(
x
)
1
x
2
+
x
-
2
;
f
(
0
)
...
Đọc tiếp
Cho hàm số f(x) xác định trên ℝ \ - 2 ; 1 thỏa mãn f ' ( x ) = 1 x 2 + x - 2 ; f ( 0 ) = 1 3 và f(3)-f(-3) = 0 Tính giá trị của biểu thức T = f(-4)+f(-1)-f(4)
![]()
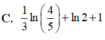
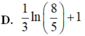
hàm số f(x)xác định trên tập số thực thỏa mãn hệ thức :f(x+1)=2f(x).Biết rằng với mọi x\(\in\)(0,1)thì f(x)=x(x-1)còn với mọi x \((\in-\infty,,m)\)
thì f(x)\(\ge\)-8/9
xác định giá trị của m từ các phương án sau đây:
A.9/4 B.7/3 C.5/2 D.8/3
giải giúp mik nha <3