Chú ý rằng nếu c > 0 thì a + b 2 + c và a + b 2 + c đều dương với mọi a, b. Áp dụng điều này chứng minh rằng:
Với mọi giá trị của x khác ± 1, biểu thức:
x + 2 x - 1 x 3 2 x + 2 + 1 - 8 x + 7 2 x 2 - 2 luôn luôn có giá trị dương.
Chú ý rằng nếu c > 0 thì a + b 2 + c và a + b 2 + c đều dương với mọi a, b. Áp dụng điều này chứng minh rằng:
Với mọi giá trị của x khác 0 và khác – 3, biểu thức:
1 - x 2 x . x 2 x + 3 - 1 + 3 x 2 - 14 x + 3 x 2 + 3 x luôn luôn có giá trị âm.
Điều kiện x ≠ 0 và x ≠ -3
Ta có:
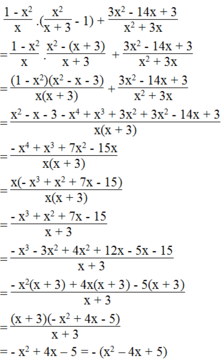
Vì x 2 - 4 x + 5 = x 2 - 4 x + 4 + 1 = x - 2 2 + 1 > 0 với mọi giá trị của x nên
- x 2 + 4 x - 5 = - x - 2 2 + 1 < 0 với mọi giá trị của x.
Vậy giá trị biểu thức luôn luôn âm với mọi giá trị x ≠ 0 và x ≠ -3
Để ý rằng: điểm B nằm giữa hai điểm A và C khi và chỉ khi A B → = t A C → , 0 < t < 1 .
Sử dụng ví dụ trên chứng minh rằng nếu điểm B nằm giữa hai điểm A và C thì điểm B’ nằm giữa hai điểm A’ và C’.
Theo ví dụ 2, ta có: A'B'→ = tA'C'→
Mà 0 < t < 1 ⇒ B' nằm giữa A' và C'
bài 2:
a) 19 và 30 b)45 và 61 c) 1,2 và 26
Mẫu:a) 19 : 30 = 0,6333 .... = 63,33%
Chú ý: Nếu phần thập phân của thương có nhiều chữ số thì chỉ lấy đến 4 chữ số
a) 19 và 30
Ta có: 19 : 30 = 0,63333...= 63,33%
b) 45 và 61
Ta có: 45 : 61 = 0,7377...= 73,77%
c) 1,2 và 26
Ta có: 1,2 : 26 = 0,046153...= 4,61%
a) 19 : 30 = 0,6333 .... = 63,33%
b)45 và 61=0,7377....=73,77%
c) 1,2 và 26 =0,0461…= 4,61%
Giả sử: x = a/m, y = b/m (a,b,m C- Z, b khác 0) và x < y. Hãy chứng tỏ rằng nếu chọn z = a+b/2m thì ta có x < z < y.
Gợi ý: Sử dụng tính chất: Nếu a,b,c C- Z và a < b thì a+c < b+c
Cho a,b,c > 0 và a+b+c=6
Chứng minh rằng : ab2 + bc2 + ca2 > (lớn hơn hoặc bằng) 24
Chú ý ab2 bc2 ca2 là ab bình phương bc bình phương và ca bình phương
2) Cho số hữu tỉ a / b với b > 0. Chứng tỏ rằng :
a) Nếu a / b > 1 thì a > b và ngược lại nếu a > b thì a / b > 1
b) Nếu a / b < 1 thì a < b và ngược lại nếu a < b thì a / b < 1
3) a) Cho 2 số hữu tỉ a / b và c / d với b > 0, d > 0. Chứng tỏ rằng nếu a / b < c / d thì: a / b < a + c / b + d < c / d
b) Viết 4 số hữu tỉ xen giữa 2 số hữu tỉ -1 / 2 và -1 / 3
Chứng minh rằng nếu a > 0 , b > 0 , c > 0 v à a < b thì a b < a + c b + c
Ta có: a b < a + c b + c
⇔ a(b + c) < (a + c)b
(vì a > 0, b > 0 và c > 0 ⇔ b + c > 0 và a + c > 0)
⇔ ab + ac < ab + bc
⇔ ac < bc ⇔ a < b (luôn đúng, theo gt)
2) Cho số hữu tỉ a / b với b > 0. Chứng tỏ rằng :
a) Nếu a / b > 1 thì a > b và ngược lại nếu a > b thì a / b > 1
b) Nếu a / b < 1 thì a < b và ngược lại nếu a < b thì a / b < 1
3) a) Cho 2 số hữu tỉ a / b và c / d với b > 0, d > 0. Chứng tỏ rằng nếu a / b < c / d thì: a / b < a + c / b + d < c / d
b) Viết 4 số hữu tỉ xen giữa 2 số hữu tỉ -1 / 2 và -1 / 3
Câu hỏi tương tự Đọc thêm
1) a) Cho a, b, thuộc Z và b khác 0. Chứng tỏ rằng: a / -b = -a / b ; -a / -b = a/b
b) So sánh các số hữu tỉ sau : -2 / 5 và 9 / -20 ; 10 / 7 và -40 / -28
2) Cho số hữu tỉ a / b với b > 0. Chứng tỏ rằng :
a) Nếu a / b > 1 thì a > b và ngược lại nếu a > b thì a / b > 1
b) Nếu a / b < 1 thì a < b và ngược lại nếu a < b thì a / b < 1
3) a) Cho 2 số hữu tỉ a / b và c / d với b > 0, d > 0. Chứng tỏ rằng nếu a / b < c / d thì: a / b < a + c / b + d < c / d
b) Viết 4 số hữu tỉ xen giữa 2 số hữu tỉ -1 / 2 và -1 / 3