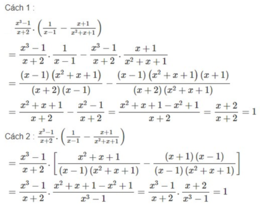Thực hiện phép nhân 1 1 - x . 1 1 + x . 1 1 + x 2 . 1 1 + x 4 . 1 1 + x 8 . 1 1 + x 16

Những câu hỏi liên quan
Trong quá trình biến đổi và tính toán những biểu thức đại số, nhiều khi ta phải thực hiện phép nhân hai đa thức một biến, chẳng hạn ta cần thực hiện phép nhân sau:
\((x - 1)({x^2} + x + 1)\)
Làm thế nào để thực hiện được phép nhân hai đa thức một biến?
Muốn nhân một đa thức với một đa thức, ta nhân mỗi đơn thức của đa thức này với từng đơn thức của đa thức kia rồi cộng các tích với nhau.
Đúng 0
Bình luận (0)
THực hiện phép nhân ; 3(x-1)(x-2)-x(3x+1)(1-x)
mình biết nội quy rồi nên đưng đăng nội quy
ai chơi bang bang 2 kết bạn với mình
mình có nick có 54k vàng đang góp mua pika
ai kết bạn mình cho
Đúng 0
Bình luận (0)
3(x - 1)(x - 2) - x(3x + 1)(1 - x)
=(3x - 3)(x - 2) - (3x^2 + x)(1 - x)
=3x^2 - 6x - 3x + 6 - (3x^2 - 3x^3 + 1 - x^2)
=3x^2 - 6x - 3x + 6 - 3x^2 +3x^3 - 1 + x^2
= -9x + 5 + x^2
Đúng 0
Bình luận (0)
BÀI 1 Thực hiện phép nhân đa thức vs đa thức
a) (x2 + 2x +1) . ( x +1)
b) (x3 - x2+2x - 1) . (5 - x)
Từ câu b) , hãy suy ra kết quả phép nhân: (x - 5) . (x3 - x2 + 2x - 1)
a) \(\left(x^2+2x+1\right)\left(x+1\right)\)
\(=x^3+x^2+2x^2+2x+x+1\)
\(=x^3+3x^2+3x+1\)
b) Ta có: \(\left(x^3-x^2+2x-1\right)\left(5-x\right)\)
\(=5x^3-x^4-5x^2+x^3+10x-2x^2-5+5x\)
\(=-x^4+6x^3-7x^2+15x-5\)
Ta có: \(\left(x-5\right)\left(x^3-x^2+2x-1\right)\)
\(=-\left(5-x\right)\left(x^3-x^2+2x-1\right)\)
\(=x^4-6x^3+7x^2-15x+5\)
Đúng 3
Bình luận (0)
Thực hiện phép nhân:
(x+3)^2=(x+3) (x+3)
(x-1)^3 =(x-1) (x-1) (x-1)
a) \(\left(x+3\right)^2=\left(x+3\right)\left(x+3\right)\)
\(\Leftrightarrow\left(x+3\right)^2=\left(x+3\right)^2\)
\(\Leftrightarrow\left(x+3\right)^2-\left(x+3\right)^2=0\)
\(\Leftrightarrow0x=0\)( luôn đúng với mọi x )
Vậy tập nghiệm của phương trình là: \(S=\left\{x\inℝ\right\}\)
b) \(\left(x-1\right)^3=\left(x-1\right)\left(x-1\right)\left(x-1\right)\)
\(\Leftrightarrow\left(x-1\right)^3=\left(x-1\right)^3\)
\(\Leftrightarrow\left(x-1\right)^3-\left(x-1\right)^3=0\)
\(\Leftrightarrow0x=0\)( luôn đúng với mọi x )
Vậy tập nghiệm của phương trình là: \(S=\left\{x\inℝ\right\}\)
Thực hiện phép nhân \((3x + 1)({x^2} - 2x + 1)\), rồi đoán xem \((3{x^3} - 5{x^2} + x + 1):(3x + 1)\) bằng đa thức nào.
\(\begin{array}{l}(3x + 1)({x^2} - 2x + 1)\\ = 3x({x^2} - 2x + 1) + 1({x^2} - 2x + 1)\\ = 3{x^3} - 6{x^2} + 3x + {x^2} - 2x + 1\\ = 3{x^3} - 5{x^2} + x + 1\end{array}\)
Vì \((3x + 1)({x^2} - 2x + 1) = 3{x^3} - 5{x^2} + x + 1\)
\( \Rightarrow (3{x^3} - 5{x^2} + x + 1):(3x + 1) = {x^2} - 2x + 1\)
Đúng 0
Bình luận (0)
Nhân đa thức với đa thức:
Thực hiện phép tính sau:
(x-1)(x+1)(x+2)
\(\left(x-1\right)\left(x+1\right)\left(x+2\right)\)
\(=\left(x^2-1\right)\left(x+2\right)\)
\(=x^3+2x^2-x-2\)
Đúng 0
Bình luận (0)
1.Nhân các đa thức sau :
a) (x+3)(x-2)
b) (x-2)(x2+4x+2)
c) (mn2-1)(m2n-4)
2.Thực hiện phép nhân :
a) (1/3s-t)(1/3s-t)
b) 9(x-1/3)(x+1/3)(9x2+1)
Thực hiện phép nhân, phép chia sau:
1/ 3a{ 2a^2 - ab }
2/ { 4 - 7b^2 }. { 2a + 5b }
Phân tích đa thức thành nhân tử:
2x^2 - 6x + xy - 3y
Tính giá trị biểu thức Q = 4x^2 - 4xy +4y^2 tại x = 3/2, y=1/3
Rút gọn phân thức A: A = 4 - 4x + x^2/3x - 6
Thực hiện phép tính:
{ 1/x+1 + 2x/1-x^2}. { 1/x-1 }
Giải giúp mình với !
Bài 1:
\(3a.\left(2a^2-ab\right)=6a^3-3a^2b\)
\(\left(4-7b^2\right).\left(2a+5b\right)=8a+20b-14ab^2-35b^3\)
Bài 2:
\(2x^2-6x+xy-3y=2x.\left(x-3\right)+y.\left(x-3\right)=\left(x-3\right).\left(2x+y\right)\)
Bài 3: Tại x = 3/2, y =1/3 thì Q = 67/9
Bài 4:
\(\left(\frac{1}{x+1}+\frac{2x}{1-x^2}\right).\left(\frac{1}{x-1}\right)\) \(\frac{1}{\left(x+1\right).\left(x-1\right)}+\frac{2x}{\left(1-x^2\right).\left(x-1\right)}=\frac{x-1}{\left(x+1\right).\left(x-1\right)^2}+\frac{-2x}{\left(x-1\right)^2.\left(x+1\right)}\)
= \(\frac{x-1-2x}{\left(x+1\right).\left(x-1\right)^2}=\frac{-\left(x+1\right)}{\left(x+1\right).\left(x-1\right)^2}=\frac{-1}{\left(x-1\right)^2}\)
Đúng 0
Bình luận (0)
Thực hiện các phép tính sau bằng hai cách: dùng tính chất phân phối của phép nhân đối với phép cộng và không dùng tính chất này:
x
3
-
1
x
+
2
.
1
x
-
1
-...
Đọc tiếp
Thực hiện các phép tính sau bằng hai cách: dùng tính chất phân phối của phép nhân đối với phép cộng và không dùng tính chất này: x 3 - 1 x + 2 . 1 x - 1 - x + 1 x 2 + x + 1
thực hiện phép tính :
a) 5x+10/10xy^2 nhân 12x/x+2
b) x-4/3x-1 nhân 9x-3/x^2-16
c)4x+2/(x+4)^2/ chia 3(x+3)/x+4
d)5x-5/3x+3 chia x-1/x+1
a: \(=\dfrac{5\left(x+2\right)}{10xy^2}\cdot\dfrac{12x}{x+2}=\dfrac{60x}{10xy^2}=\dfrac{6}{y^2}\)
b: \(=\dfrac{x-4}{3x-1}\cdot\dfrac{3\left(3x-1\right)}{\left(x-4\right)\left(x+4\right)}=\dfrac{3}{x+4}\)
c: \(=\dfrac{2\left(2x+1\right)}{\left(x+4\right)^2}\cdot\dfrac{\left(x+4\right)}{3\left(x+3\right)}=\dfrac{2\left(2x+1\right)}{3\left(x+3\right)\left(x+4\right)}\)
d: \(=\dfrac{5\left(x-1\right)}{3\left(x+1\right)}\cdot\dfrac{x+1}{x-1}=\dfrac{5}{3}\)
Đúng 0
Bình luận (0)