Độ nở khối của vật rắn đồng chất được xác định theo công thức:
![]()
![]()
![]()
![]()
Độ nở khối của vật rắn đồng chất được xác định theo công thức:
A. ∆ V = V - V 0 = β V 0 ∆ t
B. ∆ V = V - V 0 = V 0 ∆ t
C. ∆ V = β V 0
D. ∆ V = V - V 0 = β V ∆ t
Chọn A
Sự tăng thể tích của vật rắn khi nhiệt độ tăng gọi là sự nở khối.
Công thức độ nở khối: ∆ V = V - V 0 = β V 0 ∆ t
+ Độ nở dài của vật rắn tỉ lệ thuận với độ tăng nhiệt độ Δt và độ dài ban đầu l 0 của vật đó:
∆ l = l - l 0 = a l 0 ∆ t
Độ nở dài Dl của vật rắn (hình trụ đồng chất) được xác định theo công thức:
![]()
![]()
![]()
![]()
Đáp án: B
+ Độ nở dài Dl của vật rắn hình trụ đồng chất tỉ lệ với độ tăng nhiệt độ Dt và độ dài ban đầu lo của vật đó.
+ Công thức tính độ nở dài:
∆l = l – l0 = α.l0.∆t
Với lo là chiều dài ban đầu tại t0
a là hệ số nở dài của vật rắn, có đơn vị là K-1, giá trị của a phụ thuộc vào chất liệu của vật rắn.
Xét một vật rắn đồng chất, đẳng hướng và có dạng khối lập phương. Hãy chứng minh độ tăng thể tích ΔV của vật rắn này khi bị nung nóng từ nhiệt độ đầu to đến nhiệt độ t được xác định bởi công thức :
ΔV = V - Vo = βVoΔt
Với Vo và V lần lượt là thể tích của vật rắn ở nhiệt độ đầu to và nhiệt độ cuối t, Δt = t - to, β ≈ 3α (α là hệ số nở dài của vật rắn này).
Chú ý: α2 và α3 rất nhỏ so với α.
Ở nhiệt độ t0 (ºC) cạnh hình lập phương là l0
→ thể tích khối lập phương là:
Ở nhiệt độ t (ºC) cạnh hình lập phương là l
→ thể tích khối lập phương là: V = l3
Mặt khác ta có: l = l0.(1 + αΔt) ⇒ V = l03.(1 + αΔt)3
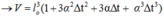
Do α rất nhỏ nên α2 và α3 cũng rất nhỏ, ta có thể bỏ qua.
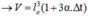
→ ΔV = V – V0 = V0.β.Δt
Xét một vật rắn đồng chất, đẳng hướng và có dạng khối lập phương. Hãy chứng minh độ tăng thể tích ΔV của vật rắn này khi bị nung nóng từ nhiệt độ đầu to đến nhiệt độ t được xác định bởi công thức:
ΔV = V - Vo = βVoΔt
Với Vo và V lần lượt là thể tích của vật rắn ở nhiệt độ đầu to và nhiệt độ cuối t, Δt = t - to, β ≈ 3α (α là hệ số nở dài của vật rắn này).
Chú ý: α2 và α3 rất nhỏ so với α.
+ Gọi V0 là thể tích của khối lập phương ở 0oC:
V0 = l03
+ V là thể tích của khối lập phương ở t0C:
V = l3 = [l0(1+ α∆t)]3 = l03 (1+α∆t)3
Mà (1+ α∆t)3 = 1 + 3α∆t + 3α2∆t2 + α3∆t3
Vì α khá nhỏ nên α2, α3 có thể bỏ qua.
=> V = l3 = l03 (1+ 3α∆t) = Vo (1+ β∆t) với β = 3α.
Để xác định khối lượng riêng của một chất tạo nên vật cần phải xác định được những đại lượng nào? Theo em, cách xác định khối lượng riêng của một vật rắn không thấm nước và của một lượng chất lỏng có khác nhau hay không?
Tham khảo!
- Để xác định khối lượng riêng của một vật rắn không thấm nước cần phải xác định được những đại lượng là khối lượng và thể tích của vật.
- Theo em, cách xác định khối lượng riêng của một vật rắn và của một lượng chất lỏng có khác nhau.
Đốt cháy một ít bột đồng trong không khí một thời gian ngắn. Sau khi kết thúc phản ứng thấy khối lượng chất rắn thu được tăng lên \(\dfrac{1}{6}\) khối lượng của bột đồng ban đầu. Hãy xác định thành phần % theo khối lượng của chất rắn thu được sau khi đun nóng
Giả sử có 1 mol Cu
=> mCu(bd) = 64 (g)
\(hh_{sau.pư}=64+\dfrac{1}{6}.64=\dfrac{224}{3}\left(g\right)\)
Gọi số mol Cu pư là a (mol)
PTHH: 2Cu + O2 --to--> 2CuO
a---------------->a
=> hh sau pư chứa \(\left\{{}\begin{matrix}CuO:a\left(mol\right)\\Cu:1-a\left(mol\right)\end{matrix}\right.\)
=> \(80a+64\left(1-a\right)=\dfrac{224}{3}\)
=> a = \(\dfrac{2}{3}\left(mol\right)\)
\(\left\{{}\begin{matrix}\%m_{Cu}=\dfrac{64\left(1-\dfrac{2}{3}\right)}{\dfrac{224}{3}}.100\%=28,57\%\\\%m_{CuO}=\dfrac{80.\dfrac{2}{3}}{\dfrac{224}{3}}.100\%=71,43\%\end{matrix}\right.\)
Câu 1 Xác định công thức phân tử của oxit sắt biết nồng độ % theo khối lượng của Fe=70% còn lại là oxi Câu 2 cho biết nồng độ % theo khối lượng của các chất trong oxit là Al=52,94% còn lại là oxi Xác định công thức phân tử Câu 3 tìm CTHH của 1 oxit biết tỉ lệ về khối lượng là \(\dfrac{m_N}{m_O}\)=\(\dfrac{7}{12}\)
Câu 1 :
\(CT:Fe_xO_y\)
\(\%O=100-70=30\%\)
\(\dfrac{\%Fe}{\%O}=\dfrac{56x}{16y}=\dfrac{70}{30}\)
\(\Rightarrow\dfrac{x}{y}=\dfrac{2}{3}\)
\(CT:Fe_2O_3\)
Câu 2 :
\(CT:Al_xO_y\)
\(\%O=100-52.94=47.06\%\)
Ta có :
\(\dfrac{27x}{16y}=\dfrac{\%Al}{\%O}=\dfrac{52.94}{47.06}\)
\(\Rightarrow\dfrac{x}{y}=\dfrac{2}{3}\)
\(CT:Al_2O_3\)
Câu 3 :
\(CT:N_xO_y\)
Ta có :
\(\dfrac{m_N}{m_O}=\dfrac{7}{12}\Rightarrow\dfrac{14x}{16y}=\dfrac{7}{12}\)
\(\Rightarrow\dfrac{x}{y}=\dfrac{2}{3}\)
\(CT:N_2O_3\)
Một vật rắn hình khối lập phương đồng chất, đẳng hướng có hệ số nở dài là α = 24.10- 6K-1. Nếu tăng nhiệt độ của vật thêm 100 o C thì độ tăng diện tích tỉ đối của mặt ngoài vật rắn là:
A. 0,36%
B. 0,48%
C. 0,4%
D. 0,45%
Ta có: ∆ S = S - S 0 = β ' S 0 ∆ t = 2 α S 0 ∆ t
=>Độ tăng diện tich tỉ đối: ∆ S S 0 = β ' ∆ t = 2 α ∆ t = 2 . 24 . 10 - 6 . 100 = 4 , 8 . 10 - 3 = 0 , 48 %
Đáp án: B
: Nhiệt phân hoàn toàn 21 gam muối cacbonat kim loại hóa trị 2 thu được chất rắn A và khí B. Toàn bộ khí B dẫn vào 200 gam dung dịch Ba(OH)2 nồng độ 17,1% thu được 29,55 gam kết tủa.
a/ Tính khối lượng chất rắn A và xác định công thức hóa học của muối cacbonat.
b/ Cho 4,2 gam muối cacbonat của kim loại hóa trị 2 ở trên vào 50 ml dung dịch HCl 3M (D = 1,15 g/ml). Tính nồng độ % của các chất trong dung dịch sau phản ứng.
a. Đặt CT muối: \(RCO_3\)
\(RCO_3\rightarrow\left(t^o\right)RO+CO_2\) (1)
\(n_{Ba\left(OH\right)_2}=\dfrac{200.17,1}{171.100}=0,2\left(mol\right)\)
\(n_{BaCO_3}=\dfrac{29,55}{197}=0,15\left(mol\right)\)
`@` TH1: Chỉ tạo ra kết tủa
\(Ba\left(OH\right)_2+CO_2\rightarrow BaCO_3\downarrow+H_2O\)
0,15 0,15 0,15 ( mol )
Theo ptr (1): \(n_{RCO_3}=n_{RO}=n_{CO_2}=0,15\left(mol\right)\)
\(M_{RCO_3}=\dfrac{21}{0,15}=140\) \((g/mol)\)
\(\Leftrightarrow R=80\) ( loại )
`@` TH2: Ba(OH)2 hết
\(Ba\left(OH\right)_2+CO_2\rightarrow BaCO_3\downarrow+H_2O\)
0,2 ( mol )
0,15 0,15 0,15 ( mol )
\(Ba\left(OH\right)_2+2CO_2\rightarrow Ba\left(HCO_3\right)_2\)
0,05 0,1 ( mol )
Theo ptr (1): \(n_{RCO_3}=n_{RO}=n_{CO_2}=0,15+0,1=0,25\left(mol\right)\)
\(M_{RCO_3}=\dfrac{21}{0,25}=84\) \((g/mol)\)
\(\Leftrightarrow R=24\) `->` R là Mg
\(n_{MgO}=0,25.\left(24+16\right)=10\left(g\right)\)
b.\(n_{MgCO_3}=\dfrac{4,2}{84}=0,05\left(mol\right)\)
\(n_{HCl}=0,05.3=0,15\left(mol\right)\)
\(m_{HCl}=50.1,15=57,5\left(g\right)\)
\(MgCO_3+2HCl\rightarrow MgCl_2+CO_2+H_2O\)
0,05 < 0,15 ( mol )
0,05 0,1 0,05 0,05 ( mol )
\(m_{ddspứ}=4,2+57,5-0,05.44=59,5\left(g\right)\)
\(\left\{{}\begin{matrix}\%m_{MgCl_2}=\dfrac{0,05.95}{59,5}.100=7,98\%\\\%m_{HCl\left(dư\right)}=\dfrac{\left(0,15-0,1\right).36,5}{59,5}.100=3,06\%\end{matrix}\right.\)