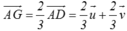Cho các vectơ u → , v → thỏa mãn u → = 5 2 , v → = 7 . Biểu thức ( u ⃗ + v ⃗ ) . ( u ⃗ - v ⃗ ) bằng
A. - 1
B. 1
C. 5 2 - 7
D. 7 - 5 2
Những câu hỏi liên quan
Trong không gian với hệ tọa độ Oxyz cho vectơ
u
→
2
;
-
1
;
2
và vectơ đơn vị
v
→
thỏa mãn
u
→
-
v
→
...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho vectơ u → = 2 ; - 1 ; 2 và vectơ đơn vị v → thỏa mãn u → - v → = 4 Độ dài của vectơ u → + v → bằng
A. 1
B. 2
C. 3
D. 4
Theo giả thiết, ta có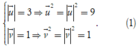 
Từ
u
→
-
v
→
=
4
, suy ra 
Kết hợp (1) và (2) ta được 
Khi đó 
Vậym | u → + v → | = 2
Chọn B.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho vectơ
u
→
2
;
-
1
;
2
và vectơ
v
→
có độ dài bằng 1 thỏa mãn
u
→
-
v
→
4...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho vectơ u → = 2 ; - 1 ; 2 và vectơ v → có độ dài bằng 1 thỏa mãn u → - v → = 4 . Độ dài của vectơ u → + v → bằng
A. 4
B. 3
C. 2
D. 1
Chọn C.
Phương pháp : Chú ý bình phương vô hướng bằng bình phương độ dài.
Đúng 0
Bình luận (0)
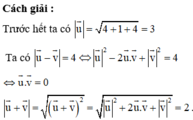
cho hình bình hành ABCD có tâm O.Gọi M,N lần lượt là trung điểm của AD,BC.Tìm tất cả các vect u thỏa mãn vectơ u = 2ON
Trong không gian Oxyz, cho đường thẳng d đi qua điểm M và có vectơ chỉ phương là
u
→
; cho đường thẳng d’ đi qua điểm M’ và có vectơ chỉ phương là
u
→
thỏa mãn
[
u
→
,
u
→
]
.
MM...
Đọc tiếp
Trong không gian Oxyz, cho đường thẳng d đi qua điểm M và có vectơ chỉ phương là u → ; cho đường thẳng d’ đi qua điểm M’ và có vectơ chỉ phương là u ' → thỏa mãn [ u → , u ' → ] . MM ' → = 0. Trong những kết luận dưới đây, kết luận nào sai?
A. d và d’ chéo nhau
B. d và d’ có thể song song với nhau
C. d và d’ có thể cắt nhau
D. d và d’ có thể trùng nhau
Đáp án A
Từ giả thiết ta suy ra hai đường thẳng d và d’ đồng phẳng, do đó khẳng định A là sai.
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ,cho vectơ u=1/2 vectơ i -5 vectơ j và vectơ v=K vectơ i -4 vectơ j a)tìm các giá trị của K để | vectơ u|=| vectơ v| Giúp tui với mng
Trong mặt phẳng toạ độ Oxy (Hình 18), cho hai vectơ overrightarrow u left( {{x_1},{y_1}} right) và overrightarrow v left( {{x_2},{y_2}} right)a) Biểu diễn các vectơ overrightarrow u ,overrightarrow v theo hai vectơ overrightarrow i và overrightarrow j b) Biểu diễn các vectơ overrightarrow u + overrightarrow v ,overrightarrow u - overrightarrow v ,koverrightarrow u left( {k in mathbb{R}} right) theo hai vectơ overrightarrow i và overrightarrow j c) Tìm tọa độ của các vectơ overrightarrow...
Đọc tiếp
Trong mặt phẳng toạ độ Oxy (Hình 18), cho hai vectơ \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\) và \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\)
a) Biểu diễn các vectơ \(\overrightarrow u ,\overrightarrow v \) theo hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \)
b) Biểu diễn các vectơ \(\overrightarrow u + \overrightarrow v \),\(\overrightarrow u - \overrightarrow v \),\(k\overrightarrow u \left( {k \in \mathbb{R}} \right)\) theo hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \)
c) Tìm tọa độ của các vectơ \(\overrightarrow u + \overrightarrow v \),\(\overrightarrow u - \overrightarrow v \),\(k\overrightarrow u \left( {k \in \mathbb{R}} \right)\)
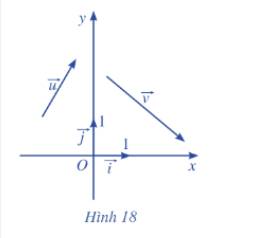
a) Do \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\), \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\) nên \(\overrightarrow u = {x_1}\overrightarrow i + {y_1}\overrightarrow j .\), \(\overrightarrow v = {x_2}\overrightarrow i + {y_2}\overrightarrow j .\)
b) +) \(\overrightarrow u + \overrightarrow v = \left( {{x_1}\overrightarrow i + {y_1}\overrightarrow j } \right) + \left( {{x_2}\overrightarrow i + {y_2}\overrightarrow j } \right) = \left( {{x_1}\overrightarrow i + {x_2}\overrightarrow i } \right) + \left( {{y_1}\overrightarrow j + {y_2}\overrightarrow j } \right) = \left( {{x_1} + {x_2}} \right)\overrightarrow i + \left( {{y_1} + {y_2}} \right)\overrightarrow j \)
+) \(\overrightarrow u - \overrightarrow v = \left( {{x_1}\overrightarrow i + {y_1}\overrightarrow j } \right) - \left( {{x_2}\overrightarrow i + {y_2}\overrightarrow j } \right) = \left( {{x_1}\overrightarrow i - {x_2}\overrightarrow i } \right) + \left( {{y_1}\overrightarrow j - {y_2}\overrightarrow j } \right) = \left( {{x_1} - {x_2}} \right)\overrightarrow i + \left( {{y_1} - {y_2}} \right)\overrightarrow j \)
+) \(k\overrightarrow u = \left( {k{x_1}} \right)\overrightarrow i + \left( {k{y_1}} \right)\overrightarrow j \)
c) Tọa độ của các vectơ \(\overrightarrow u + \overrightarrow v \),\(\overrightarrow u - \overrightarrow v \),\(k\overrightarrow u \left( {k \in \mathbb{R}} \right)\)lần lượt là:
\(\left( {{x_1} + {x_2};{y_1} + {y_2}} \right),\left( {{x_1} - {x_2};{y_1} - {y_2}} \right),\left( {k{x_1},k{y_1}} \right)\)
Đúng 0
Bình luận (0)
Cho DABC có trọng tâm G. Cho các điểm D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB và I là giao điểm của AD và EF. Đặt
u
→
A
E
→
;
v
→
A
F
→
...
Đọc tiếp
Cho DABC có trọng tâm G. Cho các điểm D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB và I là giao điểm của AD và EF. Đặt u → = A E → ; v → = A F → . Hãy phân tích các vectơ theo hai vectơ u → , v →
A. 
B. 
C. 
D. tất cả sai
Trong mặt phẳng tọa độ Oxy, cho overrightarrow u (2; - 3),;overrightarrow v (4;1),;overrightarrow a (8; - 12)a) Hãy biểu thị mỗi vectơ overrightarrow u ,;overrightarrow v ,;overrightarrow a theo các vectơ overrightarrow i ,;overrightarrow j b) Tìm tọa độ của các vectơ overrightarrow u + ;overrightarrow v ,;4.;overrightarrow u c) Tìm mối liên hệ giữa hai vectơ overrightarrow u ,;overrightarrow a
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow u = (2; - 3),\;\overrightarrow v = (4;1),\;\overrightarrow a = (8; - 12)\)
a) Hãy biểu thị mỗi vectơ \(\overrightarrow u ,\;\overrightarrow v ,\;\overrightarrow a \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \)
b) Tìm tọa độ của các vectơ \(\overrightarrow u + \;\overrightarrow v ,\;4.\;\overrightarrow u \)
c) Tìm mối liên hệ giữa hai vectơ \(\overrightarrow u ,\;\overrightarrow a \)
a) Ta có: \(\overrightarrow u = (2; - 3)\)
\( \Rightarrow \overrightarrow u = 2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j \)
Tương tự ta có: \(\overrightarrow v = (4;1),\;\overrightarrow a = (8; - 12)\)
\( \Rightarrow \overrightarrow v = 4.\;\overrightarrow i + 1.\;\overrightarrow j ;\;\;\overrightarrow a = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \)
b) Ta có: \(\left\{ \begin{array}{l}\overrightarrow u = 2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j \\\overrightarrow v = 4.\;\overrightarrow i + 1.\;\overrightarrow j \end{array} \right.\)(theo câu a)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\overrightarrow u + \;\overrightarrow v = \left( {2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j } \right) + \left( {4.\;\overrightarrow i + 1.\;\overrightarrow j } \right)\\4.\;\overrightarrow u = 4\left( {2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j } \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow u + \;\overrightarrow v = \left( {2.\;\overrightarrow i + 4.\;\overrightarrow i } \right) + \left( {\left( { - 3} \right).\;\overrightarrow j + 1.\;\overrightarrow j } \right)\\4.\;\overrightarrow u = 4.2.\;\overrightarrow i + 4.\left( { - 3} \right).\;\overrightarrow j \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow u + \;\overrightarrow v = 6.\;\overrightarrow i + \left( { - 2} \right).\;\overrightarrow j \\4.\;\overrightarrow u = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \end{array} \right.\end{array}\)
c) Vì \(\left\{ \begin{array}{l}4.\;\overrightarrow u = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \\\overrightarrow a = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \end{array} \right.\) nên ta suy ra \(4.\;\overrightarrow u = \overrightarrow a \)
Đúng 0
Bình luận (0)
Cho DABC có trọng tâm G. Cho các điểm D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB và I là giao điểm của AD và EF. Đặt
u
→
A
E
→
;
v
→
A
F
→
Hãy phân tích các vectơ
A
G
→...
Đọc tiếp
Cho DABC có trọng tâm G. Cho các điểm D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB và I là giao điểm của AD và EF. Đặt u → = A E → ; v → = A F → Hãy phân tích các vectơ A G → theo hai vectơ u → ; v →
A. A G → = 2 u → + 2 v →
B. A G → = 3 u → + 3 v →
C. A G → = 2 3 u → + 2 3 v →
D. tất cả sai
Chọn C.
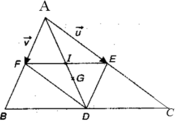
+ Ta có 
( quy tắc hình bình hành)
Do đó: 
Đúng 0
Bình luận (0)