Cho y = F ( x ) v à y = G ( x ) là những hàm số có đồ thị cho trong hình bên dưới, đặt P ( x ) = F ( x ) G ( x ) . Tính P ' ( 2 ) .
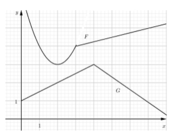
A. 5 2
B. 4
C. 3 2
D. 6
Cho sơ đồ sau:
C2H6(X) à C2H5Cl(Y) àC2H6O(Z)à C2H4O2(E) àC2H3O2Na(F) à CH4(G).
Hãy cho biết chất nào có nhiệt độ sôi và nóng chảy cao nhất?
A. Chất Z
B. Chất Y
C. Chất E
D. Chất F
Đáp án : D
X : CH3 – CH3
Y : CH3CH2Cl
Z : CH3CH2OH
E : CH3COOH
F : CH3COONa
G : CH4
Trong các chất thì hợp chất ion có nhiệt độ sôi cao nhất
Cho 2 hàm só y=f(x) và y=g(x) xác định trên R. Đặt S(x)=f(x)+g(x) và P(x)=f(x).g(x)
CMR
a,Nếu y=f(x) và y+g(x) là những hàm số lẻ thì y=S(x) là hàm số lẻ và y=P(x) là hàm số chẵn
b,Nếu y=f(x) là hàm số chẵn, y=g(x) là hàm số lẻ thì y=P(x) là hàm số lẻ
Cho hai hàm số y = f(x) và y = g(x) xác định trên R. Đặt S(x) = f(x) + g(x) và P(x) = f(x) g(x).
Xét các mệnh đề:
i) Nếu y = f(x) và y = g(x) là những hàm số chẵn thì y = S(x) và y = P(x) cũng là những hàm số chẵn
ii) Nếu y = f(x) và y = g(x) là những hàm số lẻ thì y = S(x) là hàm số lẻ và y = P(x) là hàm số chẵn
iii) Nếu y = f(x) là hàm số chẵn, y = g(x) là hàm số lẻ thì y = P(x) là hàm số lẻ
Số mệnh đề đúng là:
A. 1
B. 2
C. 3
D. Tất cả đều sai
Cho hai hàm số f(x) và g(x) liên tục trên [a;b] và thỏa mãn 0 < g ( x ) < f ( x ) , ∀ x ∈ [ a ; b ] . Gọi V là thể tích của khối tròn xoay sinh ra khi quay quanh Ox hình phẳng (H) giới hạn bởi các đường: y = f ( x ) , y = g ( x ) , x = a ; x = b . Khi đó V được tính bởi công thức nào sau đây?
A. π ∫ a b f x - g x 2 dx
B. π ∫ a b f 2 x - g 2 x dx
C. π ∫ a b f x - g x dx 2
D. ∫ a b f x - g x dx
Chọn B.
Áp dụng công thức tính thể tích khối tròn xoay: giới hạn bởi đồ thị hàm số y = f(x), y = g(x), x = a, x = b khi quay xung quanh trục Ox
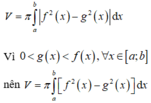
Cho hai hàm số f(x) và g(x) liên tục trên [a;b] và thỏa mãn 0 < g ( x ) < f ( x ) , ∀ x ∈ [ a ; b ] . Gọi V là thể tích của khối tròn xoay sinh ra khi quay quanh Ox hình phẳng (H) giới hạn bởi các đường: y = f ( x ) , y = g ( x ) , x = a ; x = b . Khi đó V được tính bởi công thức nào sau đây?
A. π ∫ a b f x - g x 2 dx
B. π ∫ a b f 2 x - g 2 x dx
C. π ∫ a b f x - g x dx 2
D. ∫ a b f x - g x dx
Chọn B.
Áp dụng công thức tính thể tích khối tròn xoay: giới hạn bởi đồ thị hàm số y = f(x), y = g(x), x = a, x = b khi quay xung quanh trục Ox
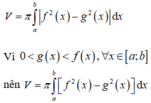
cho hàm số y=3x+1=f(x)và y=g(x)=1-3x
a tính f(-1)+g(-1)
b tìm x sao cho f(x)=g(x)
a) Thay x=-1 vào hàm số y=F(x)=3x+1, ta được
3*(-1)+1=-3+1=-2
Thay x=-1 vào hàm số y=G(x)=1-3x, ta được
1-3*(-1)=1-(-3)=1+3=4
Ta có: F(-1)+G(-1)=-2+4=2
Vậy: F(-1)+G(-1)=-2+4=2
b) Ta có: F(x)=G(x)
⇔3x+1=1-3x
⇔3x+1-1+3x=0
⇔6x=0
hay x=0
Vậy: Khi x=0 thì F(x)=G(x)
Cho hai hàm số y=f(x),y=g(x) có đạo hàm là f'(x),g'(x) Đồ thị hàm số f'(x), g'(x) được cho như hinh vẽ dưới đây
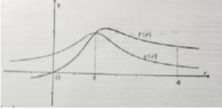
Biết rằng f(0)-f(6)<g(0)-g(6) Giá trị lớn nhất, giá trị nhỏ nhất của hàm số h(x)=f(x)-g(x) trên đoạn [0;6] lần lượt là:
A. h(6),h(2)
B. h(0),h(2)
C. h(2),h(6)
D. h(2),h(0)
cho hai hai hàm số y=f(x)=3x-2x^2 và y= g(x)=3x-2
Tính f(1),f(0),f(1/2),g(-2),f(1)+g(-2)
Tính :
f(1) = 3.1 - 2.12 = 3 - 2 = 1
f(0) = 3.0 - 2.02 = 0 - 0 = 0
\(\)f\(\left(\dfrac{1}{2}\right)=3.\dfrac{1}{2}-2.\left(\dfrac{1}{2}\right)^2=1,5-0,5=1\)
g(-2) = 3.(-2) - 2 = -8
f(1) + g(2) = 1 + (-8) = -7
Cho hai hàm số y=f(x), y=g(x) có đạo hàm là f '(x), g'(x). Đồ thị hàm số y=f '(x) và y=g(x) được cho như hình vẽ bên dưới.
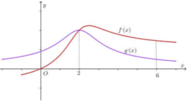
Biết rằng f 0 - f 6 < g 0 - g 6 . Giá trị lớn nhất, giá trị nhỏ nhất của hàm số h x = f x - g x trên đoạn 0 ; 6 lần lượt là:
A. h 2 ; h 6
B. h 6 ; h 2
C. h 0 ; h 2
D. h 2 ; h 0
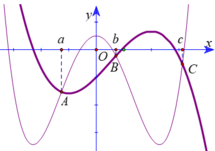
Cho hàm số y=f(x) và y=g(x) là hai hàm liên tục trên ℝ có đồ thị hàm số y = f '(x) là đường cong nét đậm và y = g(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A,B,C của y=f '(x) và y=g'(x) trên hình vẽ lần lượt có hoành độ a.b.c. Tìm giá trị nhỏ nhất của hàm số h(x) = f(x) - g(x) trên đoạn [a;c]?
![]()
![]()
![]()
![]()