Diện tích hình tròn được tính theo công thức S=\pi R^2S=πR2 trong đó RR là bán kính của hình tròn. Một hình tròn có diện tích là 12,56 cm2. Bán kính hình tròn bằng....... cm.
(Lấy giá trị của \piπ là 3,14).
Hình bên là hình nón .chiều cao là h(cm),bán kính đường tròn đáy là r(cm) và độ dài đường sinh là m(cm) thì thể tích hình nón này là:
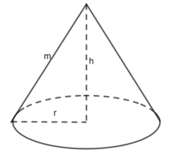
A. π . r 2 h ( c m 3 ) B. (1/3) π . r 2 h ( c m 3 )
C. π .r.m ( c m 3 ) D. π r(r+m) ( c m 3 )
Thể tích hình nón : V = (1/3) π . r 2 h ( c m 3 )
Vậy chọn đáp án B
Cho khối cầu có thể tích là 36 π ( c m 3 ). Bán kính R của khối cầu là
tính diện tích hình tròn có bán kính R=3,2cm (π = 3,14)
Diện tích hình tròn là
3,2 x 3,2 x 3,14 = 32,1536 ( cm^2)
diện tích hình tròn là:
3,2 x 3,2 x 3,14 = 32,1536 (cm2)
Cho một mặt cầu có diện tích S, thể tích khối cầu đó là V. Bán kính R của mặt cầu là:
A. R = 4V/S B. R = S/3V
C. R = 3V/S D. R = V/3S
Chọn C.
Dựa vào công thức diện tích mặt cầu và thể tích hình cầu, ta có:
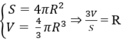
Một cái ống rỗng dạng hình trụ hở một đầu kín một đầu (độ dày không đáng kể ) dài b (cm) và bán kính đường tròn là r (cm). Nếu người ta sơn cả bên ngoài lẫn bên trong ống thì diện tích ống được sơn bao phủ là :
A.2( π r 2 +2 π rb) c m 2 B. ( π r 2 +2 π rb) c m 2
C. (2 π r 2 +2 π rb) c m 2 D. ( π r 2 +4 π rb) c m 2
Diện tích xung quanh của ống hình trụ :
S x q = 2πrb ( c m 2 )
Diện tích đáy của ống hình trụ :
S đ á y = π r 2 ( c m 2 )
Vì sơn cả bên ngoài lẫn bên trong ống nên diện tích ống được sơn bao phủ bằng hai lần diện tích xung quanh và hai lần diện tích đáy
S = 2.2 π rb + 2 π r 2 = 2( π r 2 + 2 π rb) ( c m 2 )
Vậy chọn đáp án A
Cho mặt cầu (S) có bán kính R = 5 (cm). Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 π (cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Thể tích lớn nhất của khối tự diện ABCD bằng bao nhiêu?
A. 32 3 ( c m 3 )
B. 60 3 ( c m 3 )
C. 20 3 ( c m 3 )
D. 96 3 ( c m 3 )
Một hình quạt tròn bán kính R=4/√π, cung 90°. Tính diện tích hình quạt đó
S quạt = \(\dfrac{\pi.R^{2^{ }}.n^o}{360}\)=\(\dfrac{\pi.\left(\dfrac{4}{\sqrt{\pi}}\right)^2.90}{360}\)=4(đ/v diện tích)
Cho mặt cầu có bán kính R và cho một hình trụ có bán kính đáy R, chiều cao 2R. Tỉ số diện tích mặt cầu và diện tích xung quanh của hình trụ là
A. 2 3
B. 3
C. 1
D. 1 2
Cho mặt cầu có bán kính R và cho một hình trụ có bán kính đáy R, chiều cao 2R. Tỉ số diện tích mặt cầu và diện tích xung quanh của hình trụ là
