Các câu hỏi tương tự
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h = 3 là chiều cao. Biết thể tích khối nón cụt là V = π tìm giá trị lớn nhất của biểu thức P = R + 2r.
A. 2 3
B. 3
C. 3 3
D. 2
Một mặt cầu có diện tích xung quanh là π thì có bán kính bằng
A. 3 2
B. 3
C. 1 2
D. 1
Tính diện tích của mặt cầu có bán kính r=2
A. 32 π
B. 8 π
C. 2 π
D. 16 π
Tính diện tích S của mặt cầu có bán kính R = 2.
A. S = 32 π 3
B. S = 4 π
C. S = 8 π
D. S = 16 π
Mặt cầu bán kính r có diện tích bằng 36 π . Tìm thể tích V của khối cầu bán kính r.
A. V = 72 2 π
B. V = 288 π
C. V = 36 π
D. V = 18 π
Cho mặt cầu có bán kính R và cho một hình trụ có bán kính đáy R, chiều cao 2R. Tỉ số diện tích mặt cầu và diện tích xung quanh của hình trụ là
A. 2 3
B. 3
C. 1
D. 1 2
Cho mặt cầu có bán kính R và cho một hình trụ có bán kính đáy R, chiều cao 2R. Tỉ số diện tích mặt cầu và diện tích xung quanh của hình trụ là
A. 2/3
B. 3
C. 1
D. 1/2
Cho mặt phẳng (P) cắt mặt cầu S(I;R) theo giao tuyến là đường tròn có bán kính r 3 cmhoảng cách từ I đến (P) bằng 2cm. Diện tích mặt cầu S(I;R) bằng A.
52
π
cm
2
B.
13
π
cm
2
C.
4
13
π
cm
2
D.
4
5
π
c...
Đọc tiếp
Cho mặt phẳng (P) cắt mặt cầu S(I;R) theo giao tuyến là đường tròn có bán kính r = 3 cmhoảng cách từ I đến (P) bằng 2cm. Diện tích mặt cầu S(I;R) bằng
A. 52 π cm 2
B. 13 π cm 2
C. 4 13 π cm 2
D. 4 5 π cm 2
Cho hàm số yf(x) liên tục trên R và có đồ thị như hình bên. Phương trình f(2sinx)m có đúng ba nghiệm phân biệt thuộc đoạn [-π;π] khi và chỉ khi A.
m
∈
{
-
3
;
1
}
. B.
m
∈
(
-
3
;
1
)
C.
m
∈
[
-
3
;
1
)
D.
m...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình bên. Phương trình f(2sinx)=m có đúng ba nghiệm phân biệt thuộc đoạn [-π;π] khi và chỉ khi
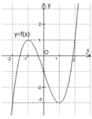
A. m ∈ { - 3 ; 1 } .
B. m ∈ ( - 3 ; 1 )
C. m ∈ [ - 3 ; 1 )
D. m ∈ ( - 3 ; 1 ]




